题目内容
命题p：?x＞0，有ln2x+lnx+1＞0，命题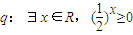
，则下列命题为真命题的是（ ）A．￢q
B．￢P∧￢q
C．P∧q
D．￢p∨￢q
【答案】分析：本题只要判断了命题p，q的真假，即可判断选择项里命题的真假．
解答：解：ln2x+lnx+1=ln2x+lnx+
+
=
＞0，对?x＞0恒成立，故命题p为真命题．
对于
，当然存在x∈R，（比如x=0时值为1），使得
，故q也为真命题．
因此，P∧q为真，
故选C
点评：本题为命题真假的判断，属基础题．
解答：解：ln2x+lnx+1=ln2x+lnx+
+=＞0，对?x＞0恒成立，故命题p为真命题．对于
，当然存在x∈R，（比如x=0时值为1），使得，故q也为真命题．因此，P∧q为真，
故选C
点评：本题为命题真假的判断，属基础题．
练习册系列答案
考前必练系列答案
相关题目
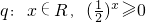，则下列命题为真命题的是