题目内容
如图(1)所示,在边长为4的正方形ABCD边上有一点P,沿着折线BCDA,由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y.

求:(1)y与x之间的函数关系式.(2)画出y=f(x)的图象.

求:(1)y与x之间的函数关系式.(2)画出y=f(x)的图象.
分析:(1)分类:当点P在BC上,当点P在CD上,当点P在DA上,分别可得三角形的面积,综合可得函数解析式;(2)由(1)的解析式,结合线段的作法可得函数图象.
解答:解:(1)当点P在BC上,即0≤x≤4时,S△ABP=
×4x=2x,
当点P在CD上,即4<x≤8时,S△ABP=
×4×4=8,
当点P在DA上,即8<x≤12时,S△ABP=
×4×(12-x)=24-2x,
∴y=
(2)由(1)的解析式y=
作函数图象,如图

| 1 |
| 2 |
当点P在CD上,即4<x≤8时,S△ABP=
| 1 |
| 2 |
当点P在DA上,即8<x≤12时,S△ABP=
| 1 |
| 2 |
∴y=
|
(2)由(1)的解析式y=
|

点评:本题考查函数解析式的求解,涉及函数图象的作法,属基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C',则在真实图形中AB边上的高是
一个水平放置的△ABC用斜二测画法画出的直观图是如图2-7-3所示的边长为1的正△A'B'C',则在真实图形中AB边上的高是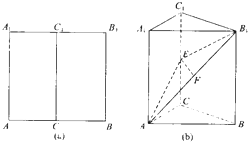 如图(a)所示,在边长为2的正方形ABB1A1中,C,C1分别是AB,A1B1的中点,现将正方形ABB1A1沿CC1折叠,使得平面ACC1A1⊥平面CBB1C1,连接AB,A1B1,AB1,如图(b)所示,F是AB1的中点,E是CC1上的点.
如图(a)所示,在边长为2的正方形ABB1A1中,C,C1分别是AB,A1B1的中点,现将正方形ABB1A1沿CC1折叠,使得平面ACC1A1⊥平面CBB1C1,连接AB,A1B1,AB1,如图(b)所示,F是AB1的中点,E是CC1上的点.
