题目内容
(本小题满分12分)已知函数f(x)=2x-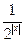 .
.
(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
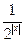 .
.(1)若f(x)=2,求x的值;
(2)若2tf(2t)+mf(t)≥0对于t∈[1,2]恒成立,求实数m的取值范围.
解:(1)当x<0时,f(x)=0;
当x≥0时,f(x)=2x- .
.
由条件可知2x- =2,即22x-2·2x-1=0,
=2,即22x-2·2x-1=0,
解得2x=1± .
.
∵2x>0,∴x=log2(1+ ).
).
(2)当t∈[1,2]时,2t +m
+m ≥0,
≥0,
即m(22t-1)≥-(24t-1).
∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],
故m的取值范围是[-5,+∞)
当x≥0时,f(x)=2x-
 .
.由条件可知2x-
 =2,即22x-2·2x-1=0,
=2,即22x-2·2x-1=0,解得2x=1±
 .
.∵2x>0,∴x=log2(1+
 ).
).(2)当t∈[1,2]时,2t
 +m
+m ≥0,
≥0,即m(22t-1)≥-(24t-1).
∵22t-1>0,∴m≥-(22t+1).
∵t∈[1,2],∴-(1+22t)∈[-17,-5],
故m的取值范围是[-5,+∞)
略

练习册系列答案
相关题目
 的图象必经过点( )
的图象必经过点( )
 题满分10分)化简或求值:
题满分10分)化简或求值:  ;
;  .
.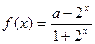 ,其中实常数
,其中实常数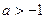 。
。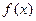 的定义域和值域;
的定义域和值域; 均为正数,且
均为正数,且 ,
, ,
, ,则( )
,则( )



 =( )
=( )
 在
在
 上的最大值与最小值之和为
上的最大值与最小值之和为  ,则其必过定点________;
,则其必过定点________;