题目内容
已知空间四边形OABC中，OA=OB，CA=CB，E、F、G、H分别为OA、OB、BC、CA的中点，求证：四边形EFGH是矩形．
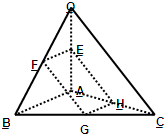
证明：∵E、F、G、H分别是OA、OB、BC、CA的中点，
∴
=
，
=
，
=
，∴EFGH是平行四边形．
•
=
•
=
(
-
)•
=
(
•
-
•
)．
∵OA=OB，CA=CB（已知），OC=OC，∴△BOC≌△AOC．∴∠BOC=∠AOC．
∴
•
=
•
，∴
•
=0，∴
⊥
，
∴四边形EFGH是矩形．
∴
| EF |
| 1 |
| 2 |
| AB |
| HG |
| 1 |
| 2 |
| AB |
| EF |
| HG |
| EF |
| EH |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| OC |
| 1 |
| 4 |
| OB |
| OA |
| OC |
| 1 |
| 4 |
| OB |
| OC |
| OA |
| OC |
∵OA=OB，CA=CB（已知），OC=OC，∴△BOC≌△AOC．∴∠BOC=∠AOC．
∴
| OB |
| OC |
| OA |
| OC |
| EF |
| EH |
| EF |
| EH |
∴四边形EFGH是矩形．
练习册系列答案
相关题目
，则△ABC一定是 （ ）