题目内容
已知函数f(x)的定义域为[-1,5],部分对应值如下表:
| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
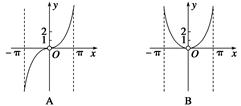
f(x)的导函数y=f′(x)的图象如图所示.

下列关于函数f(x)的命题:
①函数y=f(x)是周期函数;
②函数f(x)在[0,2]上是减函数;
③如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;
④当1<a<2时,函数y=f(x)-a有4个零点.
其中真命题的个数是( )
A.4 B.3 C.2 D.1
D
解析

练习册系列答案
相关题目
已知函数 ,若
,若 ,
,
且
 ,则
,则 ( )
( )
| A.2 | B.4 | C.8 | D.随 值变化 值变化 |
已知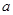 是函数
是函数 的零点,
的零点,
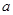 ,则
,则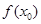 的值满足( )
的值满足( )
A.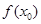 =0 =0 | B.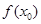 >0 >0 |
C.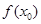 <0 <0 | D.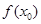 的符号不确定 的符号不确定 |
观察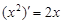 ,
,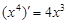 ,
,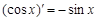 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在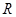 上的函数
上的函数 满足
满足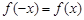 ,记
,记 为
为 的导函数,则
的导函数,则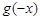 =( )
=( )
A. | B.- | C. | D.- |
下列函数中,既是偶函数,又在区间 上是减函数的是( )
上是减函数的是( )
A. | B. | C. | D. |
设函数f(x)=x|x|+bx+c,给出下列四个命题:
①c=0时,y=f(x)是奇函数;
②b=0,c>0时,方程f(x)=0只有一个实数根;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0最多有两个实根.
其中正确的命题是( )
| A.①② | B.②④ | C.①②③ | D.①②④ |
设a∈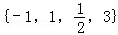 ,则使函数y=xa的定义域是R,且为奇函数的所有a的值是( )
,则使函数y=xa的定义域是R,且为奇函数的所有a的值是( )
| A.1,3 | B.﹣1,1 | C.﹣1,3 | D.﹣1,1,3 |
 在
在 内有解,则
内有解,则 的图象可能是( )
的图象可能是( )
 ,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )
,x∈(-π,0)∪(0,π)的图象可能是下列图象中的( )