题目内容
在△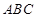 中,角
中,角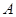 、
、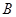 、
、 所对的边分别为
所对的边分别为 、
、 、
、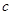 ,且
,且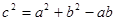 .
.
(Ⅰ)若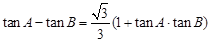 ,求角
,求角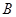 ;
;
(Ⅱ)设 ,
, ,试求
,试求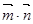 的最大值.
的最大值.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ)
【解析】
试题分析:(Ⅰ)由题中所给 ,不难想到余弦定理,可求得
,不难想到余弦定理,可求得 ,又由
,又由 ,变形成
,变形成 ,从而求出
,从而求出 ,结合
,结合 和
和 ,不难求出B; (Ⅱ)由已知可求出
,不难求出B; (Ⅱ)由已知可求出 ,又由向量的数量积公式可求出
,又由向量的数量积公式可求出 的形式,这样得到关于A的一个三角函数式,运用二倍角公式化简得一个关于
的形式,这样得到关于A的一个三角函数式,运用二倍角公式化简得一个关于 为整体的二次函数,即
为整体的二次函数,即 ,又由
,又由 的值推出
的值推出 的范围,进而得出
的范围,进而得出 的范围,从而求出
的范围,从而求出 的范围,即可求得最大值.
的范围,即可求得最大值.
试题解析:解:由 ,得
,得 ,
,
又 ,
, 3分
3分
(Ⅰ)由 ,
,
 ,
,
 ,
, 6分,
6分,
又 ,
, 8分
8分
(Ⅱ)

= 11分
11分
又 中,
中, ,得
,得 ,
, ,
,
 的最大值为
的最大值为 14分
14分
考点:1.解三角形;2.三角函数的性质;3.向量的数量积

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, .已知
.已知 .
. ;
; ,且
,且 时,求
时,求 ,
, ,
, 所对的边分别为
所对的边分别为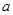 ,
, ,c.已知
,c.已知 .
.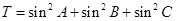 ,求T的取值范围.
,求T的取值范围. 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、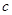 ,已知向量
,已知向量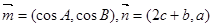 ,且
,且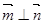 .
.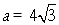 ,
, ,求△ABC的面积.
,求△ABC的面积.