题目内容
某几何体的一条棱，在该几何体的正视图中，这条棱的投影是长为
的线段，在该几何体的侧视图与俯视图中，这条棱的投影长都为
，则这条棱的长为
．
| 6 |
| 2 |
| 5 |
| 5 |
分析：由棱和它在三视图中的投影扩展为长方体，三视图中的三个投影，是三个面对角线，由此可得结论．
解答：解：由棱和它在三视图中的投影扩展为长方体，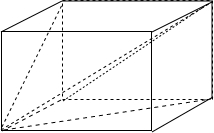
三视图中的三个投影，是三个面对角线，
则设长方体的三度：x、y、z，
所以x2+z2=6，x2+y2=2，y2+z2=2，
所以x2+y2+z2=5
∴这条棱的长为
故答案为：
三视图中的三个投影，是三个面对角线，则设长方体的三度：x、y、z，
所以x2+z2=6，x2+y2=2，y2+z2=2，
所以x2+y2+z2=5
∴这条棱的长为
| 5 |
故答案为：
| 5 |
点评：本题考查三视图，几何体的结构特征，考查空间想象能力，是中档题．
练习册系列答案
相关题目
某几何体的一条棱长为
的线段，在该几何体的侧视图与俯视图中，这条棱的投影长都为
，则这条棱的长为________．
的线段，在该几何体的侧视图与俯视图中，这条棱的投影长都为
，则这条棱的长为 ．
的线段，在该几何体的侧视图与俯视图中，这条棱的投影长都为
，则这条棱的长为 ．