题目内容
4a2+b2=1是直线 y=2x+1与椭圆
+
=1相切的( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、充要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
分析:直线与椭圆相切的充要条件是方程有一个根,联立方程组消去y得到的二次方程有一个根,判别式等于0求出充要条件.
解答:解:直线与椭圆相切等价于方程组
有且仅有一个根
即(4a2+b2)x2+4a2x+a2-a2b2=0有且仅有一个根
等价于△=16a4-4(4a2+b2)(a2-a2b2)=0
等价于4a2+b2=1
故选A
|
即(4a2+b2)x2+4a2x+a2-a2b2=0有且仅有一个根
等价于△=16a4-4(4a2+b2)(a2-a2b2)=0
等价于4a2+b2=1
故选A
点评:直线与圆锥曲线的交点个数问题等价于联立方程得到的方程组解的个数问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 +
+ =1相切的
=1相切的 +
+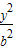 =1相切的( )
=1相切的( )