题目内容
 如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB∥DE,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB∥DE,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.(Ⅰ)求证:四点B、C、F、G共面;
(Ⅱ)求平面ADGC与平面BCGF所组成的二面角余弦值.
分析:(1)设DG的中点为M,连接AM、FM,根据条件可证明BF∥AM,BF=AM,AM∥CG,AM=CG从而得到GC∥BF,且GC=BF,根据平行线可确定一平面可得四点B、C、F、G共面;
(2)在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,根据二面角的平面角的定义可知∠MNF是所求二面角的平面角,在直角三角形MNF中,先求出此角的正切值,然后再求出余弦值.
(2)在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,根据二面角的平面角的定义可知∠MNF是所求二面角的平面角,在直角三角形MNF中,先求出此角的正切值,然后再求出余弦值.
解答:解(1)设DG的中点为M,连接AM、FM,
则由已知条件易证四边形DEFM是平行四边形,所以MF∥DE,且MF=DE
又∵AB∥DE,且AB=DE∴MF∥AB,且MF=AB
∴四边形ABMF是平行四边形,即BF∥AM,且BF=AM
又∵M为DG的中点,DG=2,AC=1,面ABC∥面DEFG
∴AC∥MG,且AC=MG,即四边形ACGM是平行四边形
∴GC∥AM,且GC=AM
故GC∥BF,且GC=BF,
即四点B、C、F、G共面;
(2)∵四边形EFGD是直角梯形,AD⊥面DEFG
∴DE⊥DG,DE⊥AD,即DE⊥面ADGC,
∵MF∥DE,且MF=DE,∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴CD=CG=
,∴cos∠DGC=
=
=
∴sin∠DGC=
,∴MN=MG•sin∠DGC=
在直角三角形MNF中,MF=2,MN
∴tan∠MNF=
=
=
,cos∠MNF=
故面ADGC与面BCGF所组成的二面角余弦值为

则由已知条件易证四边形DEFM是平行四边形,所以MF∥DE,且MF=DE
又∵AB∥DE,且AB=DE∴MF∥AB,且MF=AB
∴四边形ABMF是平行四边形,即BF∥AM,且BF=AM
又∵M为DG的中点,DG=2,AC=1,面ABC∥面DEFG
∴AC∥MG,且AC=MG,即四边形ACGM是平行四边形
∴GC∥AM,且GC=AM
故GC∥BF,且GC=BF,
即四点B、C、F、G共面;
(2)∵四边形EFGD是直角梯形,AD⊥面DEFG
∴DE⊥DG,DE⊥AD,即DE⊥面ADGC,
∵MF∥DE,且MF=DE,∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴CD=CG=
| 5 |
| GC2+GD2-CD2 |
| 2×GC× |
| 5+4-5 | ||
2×
|
| ||
| 5 |
∴sin∠DGC=
2
| ||
| 5 |
2
| ||
| 5 |
在直角三角形MNF中,MF=2,MN
2
| ||
| 5 |
∴tan∠MNF=
| MF |
| MN |
| 2 | ||||
|
| 5 |
| ||
| 6 |
故面ADGC与面BCGF所组成的二面角余弦值为
| ||
| 6 |
点评:本小题主要考查直线与直线、直线与平面、平面与平面的位置关系、相交平面所成二面角以及空间几何体的体积计算等知识,考查空间想象能力和推理论证能力、利用综合法或向量法解决立体几何问题的能力.

练习册系列答案
相关题目
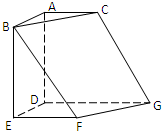 如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1. 如图,在空间直角坐标系中有长方体ABCD-A1B1C1D1,且AB=1,BC=2,AA1=2.求直线B1C与平面B1BDD1夹角的余弦值.
如图,在空间直角坐标系中有长方体ABCD-A1B1C1D1,且AB=1,BC=2,AA1=2.求直线B1C与平面B1BDD1夹角的余弦值.
