题目内容
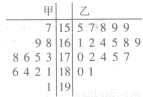
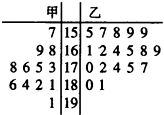 某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队员,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队员,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.(1)求甲队队员跳高成绩的中位数;
(2)如果用分层抽样的方法从甲、乙两队所有的运动员共抽取5人,则5人中“合格”与“不合格”的人数各为多少?
(3)若从所有“合格”运动员中选取2名,用X表示所选运动员中能参加市运动会开幕式旗林队的人数,试写出X的分布列,并求X的数学期望.
分析:(Ⅰ)将数据从小到大排列,即可求得中位数;
(Ⅱ)根据茎叶图,确定“合格”与“不合格”的人数,求出每个运动员被抽中的概率,即可得到X的分布列与数学期望.
(Ⅱ)根据茎叶图,确定“合格”与“不合格”的人数,求出每个运动员被抽中的概率,即可得到X的分布列与数学期望.
解答:解:(Ⅰ)中位数=
=177cm. …..(2分)
(Ⅱ)根据茎叶图,有“合格”12人,“不合格”18人,
用分层抽样的方法,每个运动员被抽中的概率是
=
,
所以选中的“合格”有12×
=2人,…..(4分)
“不合格”有18×
=3人. …..(6分)
(Ⅲ)依题意,X的取值为0,1,2.
则P(X=0)=
=
=
,P(X=1)=
=
=
,P(X=2)=
=
=
.
因此,X的分布列如下:
…..(10分)
∴EX=0×
+1×
+2×
=
=
. …..(12分)
| 176+178 |
| 2 |
(Ⅱ)根据茎叶图,有“合格”12人,“不合格”18人,
用分层抽样的方法,每个运动员被抽中的概率是
| 5 |
| 30 |
| 1 |
| 6 |
所以选中的“合格”有12×
| 1 |
| 6 |
“不合格”有18×
| 1 |
| 6 |
(Ⅲ)依题意,X的取值为0,1,2.
则P(X=0)=
| ||
|
| 28 |
| 66 |
| 14 |
| 33 |
| ||||
|
| 32 |
| 66 |
| 16 |
| 33 |
| ||
|
| 6 |
| 66 |
| 3 |
| 33 |
因此,X的分布列如下:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
∴EX=0×
| 14 |
| 33 |
| 16 |
| 33 |
| 3 |
| 33 |
| 22 |
| 33 |
| 2 |
| 3 |
点评:本题考查统计知识,考查概率的计算,考查离散型随机变量的分布列与数学期望,确定变量的取值,求出相应的概率是关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.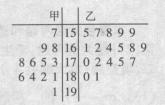
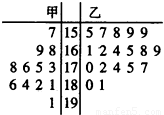 某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队员,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.
某学校为了准备参加市运动会,对本校甲、乙两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm),跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.鉴于乙队组队晚,跳高成绩相对较弱,为激励乙队队员,学校决定只有乙队中“合格”者才能参加市运动会开幕式旗林队.