题目内容

精英家教网如图，DA，CB，DC与以AB为直径的半圆分别相切于点A、B、E，且BC：AD=1：2，CD=3cm，则四边形ABCD的面积等于
 
．
分析：根据三条线段与圆相切，知道从圆外一点做圆的切线，切线长相等，再根据两者的比值，得到两条切线的长度，根据勾股定理做出圆的直径，根据梯形的面积公式得到结果．
解答：解：∵DA，CB，DC与以AB为直径的半圆分别相切于点A、B、E
∴DA=DE，CB=CE
∵BC：AD=1：2，CD=3cm
∴BC=1，AD=2，
∴圆的直径是
9-1
=2
2
，
∴四边形的面积是
(1+2)×2
2
2
=3
2

故答案为：3
2
点评：本题考查圆的切线的性质定理的证明，本题是一个典型的平面几何的求面积的题目，主要依据是圆的切线长之间的关系，运算量不大，是一个得分题目．
练习册系列答案
相关题目
如图（1）直线l∥AB，且与CA，CB分别相交于点E，F，EF与AB间的距离是d，点P是线段EF上任意一点，Q是线段AB上任意一点，则|PQ|的最小值等于d．类比上述结论我们可以得到：在图（2）中，平面α∥平面ABC，且与DA，DB，DC分别相交于点E，F，G，平面α与平面ABC间的距离是m，
a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
．
（2012•石景山区一模）如图，已知平面α∩β=l，A、B是l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，在平面α上有一个动点P，使得∠APD=∠BPC，则P-ABCD体积的最大值是（　　）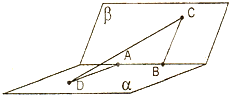
如图，甲站在水库底面上的点D处，乙站在水坝斜面上的点C处，已知测得从D、C到库底与水坝的交线的距离分别为DA=10
2
米、CB=10米，AB的长为10米，CD的长为10
6
米，则库底与水坝所成的二面角的大小为
135
135
 度．
（2012•石景山区一模）如图，已知平面α∩β=l，A、B是l上的两个点，C、D在平面β内，且DA⊥α，CB⊥α，AD=4，AB=6，BC=8，在平面α上有一个动点P，使得∠APD=∠BPC，则△PAB面积的最大值是（　　）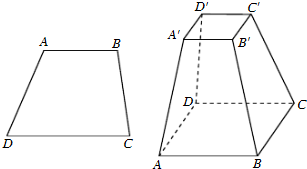
（必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
设OE=x，∵△OAB∽△ODC，∴
x
x+h
=
a
b
，即x=
ah
b-a
．
∴S梯形ABCD=S△ODC-S△OAB=
1
2
b（x+h）-
1
2
ax=
1
2
（b-a）x+
1
2
bh=
1
2
（a+b）h．
方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
设梯形AMNB的高为x，MN=y，
x
h
=
y-a
b-a
⇒y=a+
b-a
h
x，∴S梯形ABCD=
∫
h
0
（a+
b-a
h
x）dx=（ax+
b-a
2h
x2）
|
h
0
=ah+
b-a
2h
•h2=
1
2
（a+b）h．
再解下面的问题：
已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
1
3
×底面积×高）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网