题目内容
(13分)已知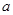 为实数,函数
为实数,函数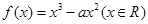 .
.
(1)若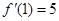 ,求
,求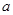 的值及曲线
的值及曲线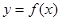 在
在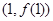 处的切线方程;
处的切线方程;
(2)求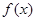 在区间
在区间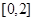 上的最大值.
上的最大值.
【答案】
解:(1)
 则
则
 ,
, 
又当 时,
时, ,
, ,
,
所以,曲线 在点
在点 处的切线方程为
处的切线方程为
 即
即 .…………………………………………(5分)
.…………………………………………(5分)
(2)令 ,解得
,解得 ,
, ,
,
当 ,即
,即 时,在
时,在 上
上 ,
, 在
在 上为增函数,
上为增函数,

当 ,即
,即 时,在
时,在 上
上 ,
, 在
在 上为减函数,
上为减函数,

当 ,即
,即 时,在
时,在 上
上 ,在
,在 上
上 ,
,
故 在
在 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,
故当 即
即 即
即 时,
时,
当 即
即 即
即 时,
时,
综上所述, ………………………………(13分)
………………………………(13分)
【解析】略

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
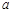 为实数,函数
为实数,函数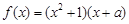 .
.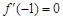 ,求函数
,求函数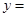
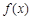 在[-
在[-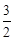 ,1]上的极大值和极小值;
,1]上的极大值和极小值;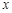 轴平行的切线,求
轴平行的切线,求 为实数,函数
为实数,函数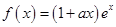 ,函数
,函数 ,
, .
. ,求函数
,求函数 的极小值;
的极小值; 时,解不等式
时,解不等式 ;
; 时,求函数
时,求函数 的单调区间.
的单调区间.