题目内容

设f（x）=sin2x+mcos2x，若对一切x∈R，都有f（x）≤f(
π
8
)，则f(
π
24
)=______．
由题意知：
f（x）=sin2x+mcos2x=
m2+1
sin（2x+φ），（sinφ=
m
m2+1
，cosφ=
1
m2+1
）
由题意得：当x=
π
8
时函数f（x）=sin2x+mcos2x取到最值±
m2+1
，
将x=
π
8
代入可得：sin（2×
π
8
）+mcos（2×
π
8
）=
2
2
(m+1)=±
m2+1
，即m=1
∴f（x）=sin2x+mcos2x=sin2x+cos2x=
2
sin（2x+
π
4
），
则f（
π
24
）=
2
sin（2×
π
24
+
π
4
）=
2
sin
π
3
=
6
2
．
故答案为：
6
2
练习册系列答案
相关题目
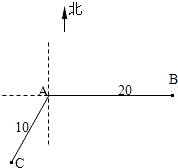精英家教网如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30°，相距10海里C处的乙船．
（Ⅰ）求处于C处的乙船和遇险渔船间的距离；
（Ⅱ）设乙船沿直线CB方向前往B处救援，其方向与
CA
成θ角，求f（x）=sin2θsinx+cos2θcosx（x∈R）的值域．
设φ∈(0，
π
4
)，函数f（x）=sin2（x+φ），且f(
π
4
)=
3
4
．
（Ⅰ）求φ的值；
（Ⅱ）若x∈[0，
π
2
]，求f（x）的最大值及相应的x值．
（2012•湖北）设函数f（x）=sin2ωx+2
3
sinωx•cosωx-cos2ωx+λ（x∈R）的图象关于直线x=π对称，其中ω，λ为常数，且ω∈（
1
2
，1）．
（1）求函数f（x）的最小正周期；
（2）若y=f（x）的图象经过点(
π
4
，0)，求函数f（x）的值域．
（2012•许昌一模）设函数f（x）=sin2（x+
π
4
）-cos2（x+
π
4
）（x∈R），则函数f（x）是（　　）
设|φ|＜
π
4
，函数f（x）=sin2（x+φ）．若f（
π
4
）=
3
4
，则φ等于（　　）
A、-
π
12
B、-
π
6
C、
π
12
D、
π
6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网