题目内容
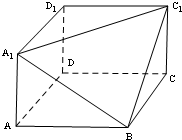 (2012•虹口区二模)在长方体ABCD-A1B1C1D1中,AB=BC=6,用过A1,B,C1三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.
(2012•虹口区二模)在长方体ABCD-A1B1C1D1中,AB=BC=6,用过A1,B,C1三点的平面截去长方体的一个角后,留下如图的几何体,且这几何体的体积为120.(1)求棱AA1的长;
(2)求点D1到平面A1BC1的距离.
分析:(1)通过长方体的体积减去三棱锥的体积直接求棱AA1的长;
(2)建立空间直角坐标系,求出A1,B,C1,D1.设平面A1BC1的法向量为
=(x,y,z),通过
得
=(2,2,3)利用d=
,求出点D1到平面A1BC1的距离.
(2)建立空间直角坐标系,求出A1,B,C1,D1.设平面A1BC1的法向量为
| n |
|
| n |
|
| ||||
|
|
解答: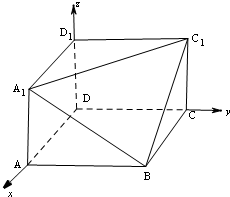 解:(1)设AA1=h,由几何体的体积关系可得:
解:(1)设AA1=h,由几何体的体积关系可得:
V=62•h-
×
×62×h=120
∴AA1=h=4…(4分)
(2)如图建立空间直角坐标系,
则A1(6,0,4),B(6,6,0),C1(0,6,4),D1(0,0,6).
设平面A1BC1的法向量为
=(x,y,z),
∴
=(0,6,-4),
=(-6,6,0),由
得
=(2,2,3)…(8分)
又
=(-6,-6,4),
∴d=
=
…(12分)
 解:(1)设AA1=h,由几何体的体积关系可得:
解:(1)设AA1=h,由几何体的体积关系可得:V=62•h-
| 1 |
| 3 |
| 1 |
| 2 |
∴AA1=h=4…(4分)
(2)如图建立空间直角坐标系,
则A1(6,0,4),B(6,6,0),C1(0,6,4),D1(0,0,6).
设平面A1BC1的法向量为
| n |
∴
| A1B |
| A1C1 |
|
| n |
又
| BD1 |
∴d=
|
| ||||
|
|
12
| ||
| 17 |
点评:本题考查几何体的体积的求法,空间直角坐标系,距离的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
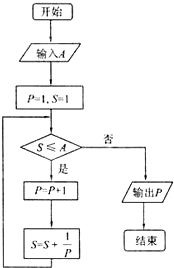 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为