题目内容
已知A={a，b，c}，B={0，1，2}，且满足f（a）+f（b）=f（c）的映射f，A→B有______个．
因为：A={a，b，c}，B={0，1，2}，且满足f（a）+f（b）=f（c），
所以分为3种情况：f（c）=0 或者f（c）=1或者f（c）=2．
当f（c）=0时，只有一个映射：f（a）=0，f（b）=0；
当f（c）=1时，有C21=2个映射；
当f（c）=2时，有C21+C11=3个映射；
因此所求的映射的个数为1+2+3=6．
故答案为6．
所以分为3种情况：f（c）=0 或者f（c）=1或者f（c）=2．
当f（c）=0时，只有一个映射：f（a）=0，f（b）=0；
当f（c）=1时，有C21=2个映射；
当f（c）=2时，有C21+C11=3个映射；
因此所求的映射的个数为1+2+3=6．
故答案为6．
练习册系列答案
相关题目
已知a=log2
，b=(
)
，c=lg3，则（ ）
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 5 |
| A、a＜b＜c |
| B、c＜a＜b |
| C、a＜c＜b |
| D、b＜c＜a |
选择题：
(1)
已知
，
，
，则
[
]|
(A)A 、B、D三点共线 |
(B)A 、B、C三点共线 |
|
(C)B 、C、D三点共线 |
(D)A 、C、D三点共线 |
(2)
已知正方形ABCD的边长为1，
，
，
，则
等于
[
]|
(A)0 |
(B)3 |
(C) |
(D) |
(3)
已知
，
，
，
，且四边形ABCD为平行四边形，则
[
]|
(A)a ＋b＋c＋d＝0 |
(B)a －b＋c－d＝0 |
|
(C)a ＋b－c－d＝0 |
(D)a －b－c＋d＝0 |
(4)
已知D、E、F分别是△ABC的边BC、CA、AB的中点，且
，
，
，则①
；②
；③
；④
中正确的等式的个数为
[
]|
(A)1 |
(B)2 |
(C)3 |
(D)4 |
(5)
若
，
是夹角为60°的两个单位向量，则
；
的夹角为
[
]|
(A)30° |
(B)60° |
(C)120° |
(D)150° |
(6)
若向量a、b、c两两所成的角相等，且
，
，
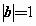，则
等于
[
]|
(A)2 |
(B)5 |
(C)2 或5 |
(D)  |
(7)
等边三角形ABC的边长为1，
，
，
，那么a·b＋b·c＋c·a等于
[
]|
(A)3 |
(B) －3 |
(C) |
(D) |
