题目内容
8.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点到它的渐近线距离为$\sqrt{3}$,直线x=-$\frac{{a}^{2}}{c}$(c为半焦距)与抛物线y2=2x的准线重合,则该双曲线的离心率为$\sqrt{6}$.分析 利用焦点到它的渐近线距离为$\sqrt{3}$,求出b,利用抛物线y2=2x的准线方程为x=-$\frac{1}{2}$,$\frac{{a}^{2}}{c}$=$\frac{1}{2}$,可得a,c,即可求出双曲线的离心率.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的方程为bx+ay=0,
∵焦点到它的渐近线距离为$\sqrt{3}$,
∴$\frac{bc}{\sqrt{{b}^{2}+{a}^{2}}}$=$\sqrt{3}$,即b=$\sqrt{3}$,
抛物线y2=2x的准线方程为x=-$\frac{1}{2}$,∴$\frac{{a}^{2}}{c}$=$\frac{1}{2}$,
∴c=3,a=$\frac{\sqrt{6}}{2}$
∴双曲线的离心率为e=$\frac{c}{a}$=$\sqrt{6}$,
故答案为:$\sqrt{6}$.
点评 本题考查双曲线的离心率,考查抛物线的性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16.下列表述中错误的是( )
| A. | 归纳推理是由特殊到一般的推理 | B. | 演绎推理是由一般到特殊的推理 | ||
| C. | 类比推理是由特殊到一般的推理 | D. | 类比推理是由特殊到特殊的推理 |
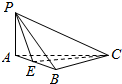 如图,三棱锥P-ABC中,△PAB是正三角形,E是AB的中点,AB⊥BC,平面PAB⊥平面ABC.若AB=2,BC=$\sqrt{2}$,则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$.
如图,三棱锥P-ABC中,△PAB是正三角形,E是AB的中点,AB⊥BC,平面PAB⊥平面ABC.若AB=2,BC=$\sqrt{2}$,则点A到平面PEC的距离是$\frac{\sqrt{6}}{3}$. 已知函数f(x)=x|x-m|,x∈R,且f(4)=0.
已知函数f(x)=x|x-m|,x∈R,且f(4)=0.