题目内容
若θ∈[0，2π），
=(cosθ，sinθ)，
=(3-cosθ，4-sinθ)，则
的取值范围是（ ）
| OP1 |
| OP2 |
| |P1P2| |
| A、[4，7] |
| B、[3，7] |
| C、[3，5] |
| D、[5，6] |
分析：利用求向量的模的方法，两角和差的正弦公式可得
=
，由-1≤sin（θ+∅）≤1，可得 9≤29-20sin（θ+∅）≤49，从而得到
的取值范围．
| |P1P2| |
| 29-20sin(θ+∅) |
| |P1P2| |
解答：解：
=|
-
|=|（3-2cosθ，4-2sinθ）|=
=
=
，
其中，tan∅=
，∅为锐角．
∵θ∈[0，2π），∴-1≤sin（θ+∅）≤1，∴9≤29-20sin（θ+∅）≤49，
∴3≤
≤7，故
的取值范围是[3，7]，
故选B．
| |P1P2| |
| OP2 |
| OP1 |
| (3-2cosθ )2+(4-2sinθ)2 |
=
| 29-12cosθ-16sinθ |
| 29-20sin(θ+∅) |
其中，tan∅=
| 3 |
| 4 |
∵θ∈[0，2π），∴-1≤sin（θ+∅）≤1，∴9≤29-20sin（θ+∅）≤49，
∴3≤
| 29-20sin(θ+∅) |
| |P1P2| |
故选B．
点评：本题考查两角和差的正弦公式的应用，正弦函数的值域，求向量的模的方法，得到 9≤29-20sin（θ+∅）≤49，
是解题的关键．
是解题的关键．
练习册系列答案
相关题目
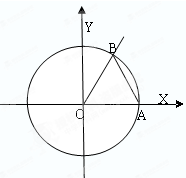如图，在平面直角坐标系xoy中，角α的始边与x轴的非负半轴重合且与单位圆相交于A点，它的终边与单位圆相交于x轴上方一点B，始边不动，终边在运动．