题目内容
(本题满分12分)已知向量
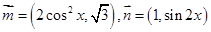 ,函数
,函数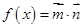
(1)求函数 的单调增区间;
的单调增区间;
(2)在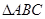 中,
中,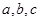 分别是角A, B, C的对边,且
分别是角A, B, C的对边,且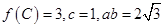 ,且
,且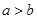
求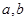 的值.
的值.
(1) (2)
(2)
解析试题分析:(1) ……3分
……3分
令 ,解得
,解得 ,
, 函数
函数 的单调增区间为
的单调增区间为 . ……6分
. ……6分
(2)
 ,
,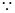
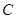 是三角形的内角,
是三角形的内角,
 则
则 , ……8分
, ……8分
 即:
即: . ……9分
. ……9分
又 ,解得:
,解得: ,则
,则

 , ……11分
, ……11分
又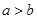 ,所以
,所以 . ……12分
. ……12分
考点:本小题主要考查三角函数的化简和三角函数性质的应用,以及余弦定理的应用,考查学生的转化能力和运算求解能力.
点评:三角函数中公式比较多,应用的时候要灵活选择,还要注意公式的应用条件,另外,三角函数的图象和性质是高考经常考查的内容,要给予充分的重视.

练习册系列答案
相关题目
已知e1,e2是夹角为60°的两个单位向量,若a=e1+e2,b=-4e1+2e2,则a与b的夹角为( ).
| A.30° | B.60° | C.120° | D.150° |
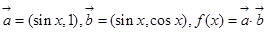
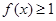 ,求x的范围;
,求x的范围;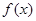 的最大值以及此时x的值.
的最大值以及此时x的值. ,
, ,
, ,
, 为坐标原点.
为坐标原点. ,求
,求 的值;;
的值;; ,且
,且 ,求
,求 与
与 的夹角.
的夹角. 与
与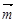 =(1,1)共线。
=(1,1)共线。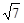 或x>
或x>
 ,其中向量
,其中向量 ,
, ,且函数
,且函数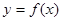 的图象经过点
的图象经过点 .
. 的值; (2)求函数
的值; (2)求函数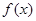 的最小值及此时
的最小值及此时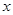 的值的集合.
的值的集合.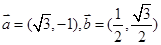
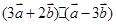 的值;
的值;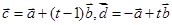 ,且
,且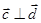 ,求实数t的值.
,求实数t的值. ,
, ,若
,若 .
. 的最小正周期;
的最小正周期;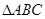 的三内角
的三内角 的对边分别为
的对边分别为 ,且
,且 ,
, (A为锐角),
(A为锐角), ,求
,求 的值.
的值.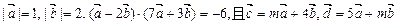 ,
,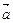 和
和 的夹角;
的夹角;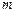 取何值时,
取何值时,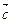 与
与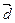 共线?
共线?