题目内容
18.已知椭圆的中心在坐标原点,焦点在x轴上,且长轴长为12,离心率为$\frac{1}{2}$,则椭圆方程为( )| A. | $\frac{{x}^{2}}{144}$+$\frac{{y}^{2}}{108}$=1 | B. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{32}$=1 | C. | $\frac{{x}^{2}}{32}$+$\frac{{y}^{2}}{36}$=1 | D. | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1 |
分析 设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意可得a=6,c=3,由a,b,c的关系,可得b,进而得到椭圆方程.
解答 解:设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由长轴长为12,离心率为$\frac{1}{2}$,
可得2a=12,e=$\frac{c}{a}$=$\frac{1}{2}$,b2=a2-c2,
解得a=6,c=3,b=3$\sqrt{3}$,
即有椭圆的方程为$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{27}$=1.
故选:D.
点评 本题考.查椭圆的方程的求法,注意运用椭圆的性质,主要是离心率公式的运用及a,b,c的关系,考查运算能力,属于基础题

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
8.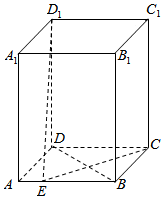 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,侧棱AA1⊥底面ABCD,已知AB=1,${A}{{A}_1}=\sqrt{3}$,E为AB上一个动点,则D1E+CE的最小值为( )| A. | $2\sqrt{2}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}+1$ | D. | $2+\sqrt{2}$ |
6.某产品在某零售摊位的零售价x(单位:元)与每天的销售量y(单位:个)的统计资料如表所示:
由表可得回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$=-4,据此模型预测零售价为20元时,每天的销售量为 ( )
| x | 16 | 17 | 18 | 19 |
| y | 50 | 34 | 41 | 31 |
| A. | 26个 | B. | 27个 | C. | 28个 | D. | 29个 |
3.设椭圆的标准方程为$\frac{x^2}{9-k}+\frac{y^2}{5-k}=1$,若焦点在x轴上,则实数k的取值范围是( )
| A. | k>5 | B. | 5<k<9 | C. | k<5 | D. | k>9 |
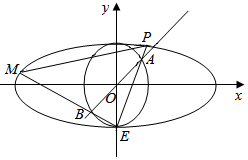 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.