题目内容
已知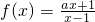 ,x∈(1,+∞),f(2)=3
,x∈(1,+∞),f(2)=3
(1)求a;
(2)判断并证明函数单调性.
解:(1)∵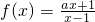 ,x∈(1,+∞),f(2)=3
,x∈(1,+∞),f(2)=3
∴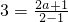 ,
,
解得a=1.
(2)∴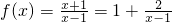 .
.
函数 在区间(1,+∞)是单调减函数.理由如下:
在区间(1,+∞)是单调减函数.理由如下:
设1<x1<x2,f(x2)-f(x1)=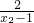 -
-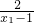 =
=
因为1<x1<x2,,所以x1-x2<0,x1-1>0,x2-1>0,
所以f(x2)-f(x1)<0,即f(x2)<f(x1)
所以函数 在区间(1,+∞)是单调减函数.
在区间(1,+∞)是单调减函数.
分析:(1)由已知中函数的解析式,将x=2,f(2)=3代入构造a的方程,解方程可得答案.
(2)任取1<x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.
点评:本题主要考查的知识点是函数单调性的判断与证明,其中作差法(定义法)证明函数的单调性是我们中学阶段证明函数单调性最重要的方法,一定要掌握其解的格式和步骤.
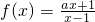 ,x∈(1,+∞),f(2)=3
,x∈(1,+∞),f(2)=3∴
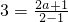 ,
,解得a=1.
(2)∴
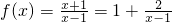 .
.函数
 在区间(1,+∞)是单调减函数.理由如下:
在区间(1,+∞)是单调减函数.理由如下:设1<x1<x2,f(x2)-f(x1)=
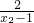 -
-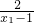 =
=
因为1<x1<x2,,所以x1-x2<0,x1-1>0,x2-1>0,
所以f(x2)-f(x1)<0,即f(x2)<f(x1)
所以函数
 在区间(1,+∞)是单调减函数.
在区间(1,+∞)是单调减函数.分析:(1)由已知中函数的解析式,将x=2,f(2)=3代入构造a的方程,解方程可得答案.
(2)任取1<x1<x2,我们构造出f(x2)-f(x1)的表达式,根据实数的性质,我们易出f(x2)-f(x1)的符号,进而根据函数单调性的定义,得到答案.
点评:本题主要考查的知识点是函数单调性的判断与证明,其中作差法(定义法)证明函数的单调性是我们中学阶段证明函数单调性最重要的方法,一定要掌握其解的格式和步骤.

练习册系列答案
相关题目