题目内容
已知数列{an}的前n项和为Sn,且 对一切正整数n成立
对一切正整数n成立
(1)求出数列{an}的通项公式;
(2)设 ,求数列
,求数列 的前n项和
的前n项和 .
.
 对一切正整数n成立
对一切正整数n成立(1)求出数列{an}的通项公式;
(2)设
 ,求数列
,求数列 的前n项和
的前n项和 .
.(1) (2)
(2)
 (2)
(2)
试题分析:(1)
 于是可利用
于是可利用 与
与 的关系求得数列
的关系求得数列 的递推公式
的递推公式 得到数列
得到数列 是等比数列,从而求得数列
是等比数列,从而求得数列 的通项公式;
的通项公式;(2)根据数列
 的通项公式
的通项公式 的特点,对其前
的特点,对其前 项的和采用拆项求和的办法、
项的和采用拆项求和的办法、 =
=
=

前一部分用错位相减法求和,后一部分正是等差数的前
 项和,从而求得
项和,从而求得 .
.试题解析:
解:(1)由已知得
 ,于是可利用
,于是可利用 与
与 的关系求得数列
的关系求得数列 的递推公式
的递推公式两式相减并整理得:

所以
 ,又
,又 ,可知
,可知 ,进而可知
,进而可知
所以
 ,故数列
,故数列 是首项为6,公比为2的等比数列,
是首项为6,公比为2的等比数列,所以
 ,即
,即
(2)

设
 ①
①则
 ②
②由②-①得:
 =
=


练习册系列答案
相关题目
 ,求证:
,求证: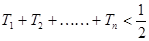 .
.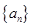 的前
的前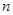 项和为
项和为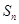 ,且
,且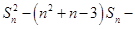
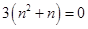 ,
,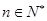 .
.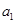 的值;
的值;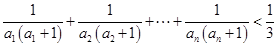 .
. 与
与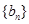 满足
满足 ,且
,且 ,设数列
,设数列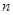 项和为
项和为 ,则
,则 =.
=.