题目内容
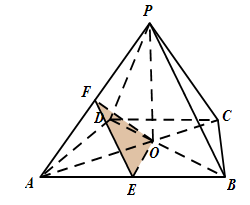
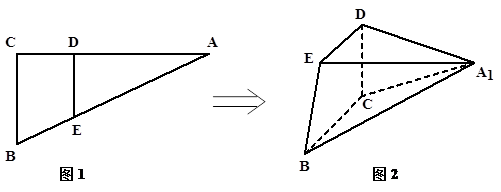
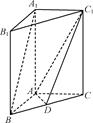
已知四棱锥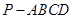 的底面
的底面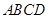 是等腰梯形,
是等腰梯形,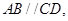 且
且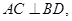
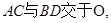
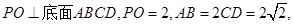
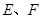 分别是
分别是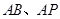 的中点.
的中点.
(1)求证: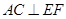 ;
;
(2)求二面角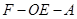 的余弦值.
的余弦值.
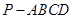 的底面
的底面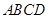 是等腰梯形,
是等腰梯形,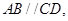 且
且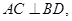
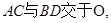
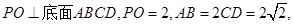
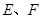 分别是
分别是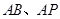 的中点.
的中点.
(1)求证:
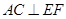 ;
;(2)求二面角
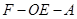 的余弦值.
的余弦值.(1)详见解析;(2)

试题分析:(1)可证
 面
面 得
得 ,因为
,因为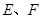 分别是
分别是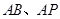 的中点
的中点 即可证
即可证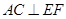 。(2)以
。(2)以 所在直线为x轴,y轴,z轴建立空间直角坐标系,先求各点的坐标然后求向量的坐标,再求面
所在直线为x轴,y轴,z轴建立空间直角坐标系,先求各点的坐标然后求向量的坐标,再求面 的一个法向量。由已知可知
的一个法向量。由已知可知 为面
为面 的一个法向量,用向量的数量积公式求两法向量所成角的余弦值。两法向量所成的角与所求二面角的平面角相等或互补。
的一个法向量,用向量的数量积公式求两法向量所成角的余弦值。两法向量所成的角与所求二面角的平面角相等或互补。试题解析:(1)
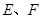 分别是
分别是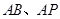 的中点.
的中点. 2分
2分由已知可知
 3分
3分

 4分
4分又

 5分
5分 6分
6分(2)以
 所在直线为x轴,y轴,z轴,
所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系. 7分

由题设,
 , 得
, 得
 8分
8分设平面
 的法向量为
的法向量为
 可取
可取 , 10分
, 10分平面
 的法向量为
的法向量为 11分
11分 13分
13分由图形可知,二面角
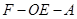 的余弦值为
的余弦值为 14分
14分
练习册系列答案
相关题目
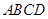 的顶点
的顶点 分别在两两垂直的三条射线
分别在两两垂直的三条射线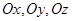 上,则在下列命题中,错误的为( )
上,则在下列命题中,错误的为( )
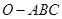 是正三棱锥
是正三棱锥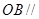 平面
平面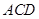
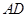 与
与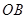 所成的角是
所成的角是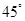
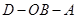 为
为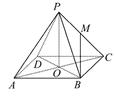

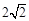
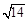
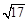
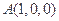 的距离除以到
的距离除以到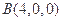 的距离的值为
的距离的值为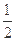 的点
的点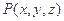 的坐标满足( )
的坐标满足( )