题目内容

如图，A，B,C是圆O上三个点，AD是∠BAC的平分线，交圆O于点D，过B作圆O的切线交AD的延长线于E．

（Ⅰ）求证：∠EBD=∠CBD；

（II）求证：AB·DE=CD·BE．

 

【答案】

（Ⅰ）先得到（II）要先证明∽

【解析】

试题分析：证明:(Ⅰ)是圆的切线,,

又为所对的圆周角,,

而是的平分线,, .  

(Ⅱ),,∽,,

又,,

,即.    

考点：几何证明

点评：在几何证明中，要证明关于四段线段的等式成立，只需找到四段线段所在的两个三角形，然后证明它们相似就好。

 

练习册系列答案
相关题目
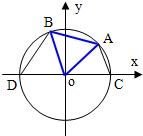精英家教网如图，A、B是单位圆O上的点，C、D分别是圆O与x轴的两个交点，△ABO为正三角形．
（1）若点A的坐标为(
3
5
，
4
5
)，求cos∠BOC的值；
（2）若∠AOC=x（0＜x＜
2π
3
），四边形CABD的周长为y，试将y表示成x的函数，并求出y的最大值．
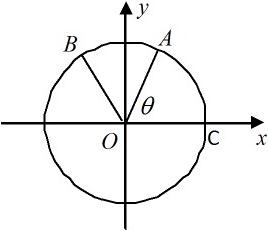精英家教网如图：A、B是单位圆上的动点，C是单位圆与x轴正半轴的交点，
且∠AOB=
π
6
，记∠COA=θ，θ∈（0，π），△AOC的面积为S．
（Ⅰ）设（θ）=OB→•OC→+2S，求f（θ）的最大值以及此时θ的值；
（Ⅱ）当A点坐标为(-
3
5
，
4
5
)时，求|
BC
|2的值．
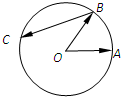如图，A，B是半径为1的圆O上两点，且∠AOB=
π
3
．若点C是圆O上任意一点，则
OA
•
BC
的取值范围为
[-
3
2
，
1
2
]
[-
3
2
，
1
2
]
．
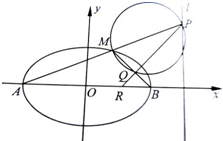如图，A，B是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左右顶点，M是椭圆上异于A，B的任意一点，若椭圆C的离心率为
1
2
，且右准线l的方程为x=4．
（1）求椭圆C的方程；
（2）设直线AM交l于点P，以MP为直径的圆交直线MB于点Q，试证明：直线PQ与x轴的交点R为定点，并求出R点的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网