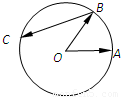
题目内容
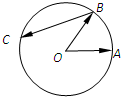 如图,A,B是半径为1的圆O上两点,且∠AOB=
如图,A,B是半径为1的圆O上两点,且∠AOB=| π |
| 3 |
| OA |
| BC |
[-
,
]
| 3 |
| 2 |
| 1 |
| 2 |
[-
,
]
.| 3 |
| 2 |
| 1 |
| 2 |
分析:建立直角坐标系,设出C的坐标,求出
,
向量,然后化简
•
,即可求解它的范围.
| OA |
| BC |
| OA |
| BC |
解答:解:以OA所在直线为x轴,OA的垂线为y轴,则A(1,0),B(
,
).
设C(cosθ,sinθ),
=(1,0),
=(cosθ-
,sinθ-
),θ∈R
所以
•
=(1,0)•(cosθ-
,sinθ-
)=cosθ-
∈[-
,
].
故答案为:[-
,
].
| 1 |
| 2 |
| ||
| 2 |
设C(cosθ,sinθ),
| OA |
| BC |
| 1 |
| 2 |
| ||
| 2 |
所以
| OA |
| BC |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故答案为:[-
| 3 |
| 2 |
| 1 |
| 2 |
点评:本题考查向量数量积的应用,考查转化思想计算能力,建立直角坐标系,利用坐标运算是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
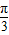 .若点C是圆O上任意一点,则
.若点C是圆O上任意一点,则 的取值范围为 .
的取值范围为 .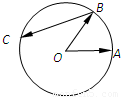
 .若点C是圆O上任意一点,则
.若点C是圆O上任意一点,则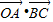 的取值范围为 .
的取值范围为 .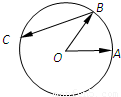
 .若点C是圆O上任意一点,则
.若点C是圆O上任意一点,则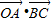 的取值范围为 .
的取值范围为 .
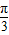 .若点C是圆O上任意一点,则
.若点C是圆O上任意一点,则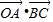 的取值范围为 .
的取值范围为 .