题目内容

设a、b、c依次是△ABC的角A、B、C所对的边，若
tanA•tanB
tanA+tanB
=1004tanC，且a2+b2=mc2，则m=______．
△ABC中，∵
tanA•tanB
tanA+tanB
=1004tanC，∴
sinAsinB
sinAcosB+cosAsinB
=1004
sinC
cocC
，
∴sinAsinBcosC=1004sinC•sin（A+B）=1004sin2C，由正弦定理得
abcosC=1004c2，c2=
abcosC
1004
． 
又∵a2+b2=mc2，∴a2+b2=m•
abcosC
1004
=
mab•
a2+b2-c2
2ab
1004
=
m(a2+b2-c2)
2008
，
∴m=
2008(a2+b2)
a2+b2-c2
=
2008(a2+b2)
a2+b2-
a2+b2
m
，∴2008（a2+b2）=m（a2+b2）-（ a2+b2 ）．
∴m=2009，
故答案为：2009．
练习册系列答案
相关题目
设a，b，c依次是方程2x+x=0，log2x=2-x，log
1
2
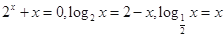x=x的根，则（　　）
设a，b，c依次是方程log
1
2
x+2=x，log2（x+2）=
-x
，2x+x-2=0的根，则a，b，c的大小关系是（　　）
（2009•黄冈模拟）设a、b、c依次是△ABC的角A、B、C所对的边，若
tanA•tanBtanA+tanB
=1004tanC，且a2+b2=mc2，则m=
2009
2009
．

设a，b，c依次是方程的根，则（    ）

A.    B.     C.      D.

 
设a，b，c依次是方程2x+x=0，log2x=2-x，x=x的根，则（ ）
A．a＞b＞c
B．a＞c＞b
C．b＞a＞c
D．b＞c＞a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网