题目内容
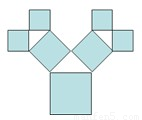
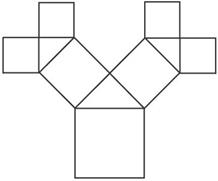
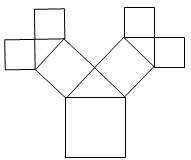 如图所示是毕达哥拉斯的生长程序:正方形一边上连接着等腰直角三角形,等腰直角三角形两直角边再分别连接着一个正方形,如此继续下去,共得到127个正方形.若最后得到的正方形的边长为1,则初始正方形的边长为
如图所示是毕达哥拉斯的生长程序:正方形一边上连接着等腰直角三角形,等腰直角三角形两直角边再分别连接着一个正方形,如此继续下去,共得到127个正方形.若最后得到的正方形的边长为1,则初始正方形的边长为8
8
.分析:由初始的一个正方形,第一次增长2个正方形,第两次增长4个正方形,…,总结第n次增长2n个正方形,发现正方形的总个数其组成的数列是以1为首项,2为公比的等比数列,根据正方形的总个数为127个,利用等比数列的求和公式列出关于n的方程,求出方程的解得到n的值,再设初始正方形的边长为a,根据其中的三角形为等腰直角三角形,可得出最后正方形边长与初始正方形边长的关系,由最后正方形的边长为1即可求出初始正方形的边长.
解答:解:第一次增长2个正方形,第二次增长4个正方形,…,第n次增长2n个正方形,
∴1+2+22+…+2n=127,即
=127,解得n=6,
设初始正方形的边长为a,
则a=
=8.
故答案为:8
∴1+2+22+…+2n=127,即
| 1-2n+1 |
| 1-2 |
设初始正方形的边长为a,
则a=
| 1 | ||||
(
|
故答案为:8
点评:此题考查了等比数列的前n项和公式,以及等比数列的通项公式,根据题意总结得出一般性的规律是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
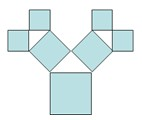 如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形…,如此继续.若共得到1023个正方形,设起始正方形的边长为
如图所示是毕达哥拉斯的生长程序:正方形上连接着一个等腰直角三角形,等腰直角三角形的直角边上再连接正方形…,如此继续.若共得到1023个正方形,设起始正方形的边长为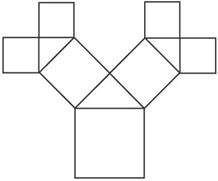
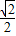 ,则最小正方形的边长为 .
,则最小正方形的边长为 .