题目内容
在△ABC的三个内角A、B、C所对的边分别a、b、c，B=
，a=2csinA．
（Ⅰ）求角C的大小；
（Ⅱ）当x∈[0，
]时，求函数f（x）=sin2x+4cosAcos2x的最大值．
| 2π |
| 3 |
（Ⅰ）求角C的大小；
（Ⅱ）当x∈[0，
| π |
| 2 |
分析：（Ⅰ）由a=2csinA，由正弦定理，即可求角C的大小；
（Ⅱ）利用二倍角公式、辅助角公式化简函数，再利用三角函数的性质，即可得到结论．
（Ⅱ）利用二倍角公式、辅助角公式化简函数，再利用三角函数的性质，即可得到结论．
解答：解：（Ⅰ）因为a=2csinA，由正弦定理得sinA=2sinCsinA，…（2分）
因为A∈（0，π），所以sinA≠0，解得sinC=
． …（4分）
又因为B=
，所以C∈(0，
)，所以C=
．…（6分）
（Ⅱ）由（Ⅰ）知，A=
．…（8分）
所以f(x)=sin2x+2
cos2x=sin2x+
(1+cos2x)=sin2x+
cos2x+
=2sin(2x+
)+
．…（11分）
因为x∈[0，
]，所以2x+
∈[
，
]，
所以f（x）的最大值是2+
．…（13分）
因为A∈（0，π），所以sinA≠0，解得sinC=
| 1 |
| 2 |
又因为B=
| 2π |
| 3 |
| π |
| 2 |
| π |
| 6 |
（Ⅱ）由（Ⅰ）知，A=
| π |
| 6 |
所以f(x)=sin2x+2
| 3 |
| 3 |
| 3 |
| 3 |
=2sin(2x+
| π |
| 3 |
| 3 |
因为x∈[0，
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
所以f（x）的最大值是2+
| 3 |
点评：本题考查正弦定理，考查三角函数的化简，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
．设函数f（x）=sin2x+4cosAcos2x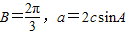
．设函数f（x）=sin2x+4cosAcos2x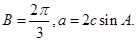
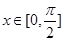时，求函数
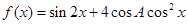的最大值