题目内容
10. 设定义域为R的函数f(x)=$\left\{\begin{array}{l}{x+1,(x≤0)}\\{{x}^{2}-2x+1,(x>0)}\end{array}\right.$.
设定义域为R的函数f(x)=$\left\{\begin{array}{l}{x+1,(x≤0)}\\{{x}^{2}-2x+1,(x>0)}\end{array}\right.$.(1)在如图所示的平面直角坐标系内作出函数f(x)的图象,并写出函数f(x)的单调区间(不需证明);
(2)求函数f(x)在区间[1,4]上的最大值与最小值.
分析 (1)根据函数解析式,可得函数的图象,根据图象写出函数f(x)的单调区间;
(2)根据图象的性质,求出结果.
解答  解:(1)如图,单调增区间为(-∞,0),(1,+∞);
解:(1)如图,单调增区间为(-∞,0),(1,+∞);
单调减区间为(0,1);
(2)函数在区间[1,4]上单调递增,f(x)min=f(1)=0,
f(x)max=f(4)=9
点评 本题考查的知识要点:分段函数的图象,函数的最值及相关的运算问题.

练习册系列答案
相关题目
15.全集U={1,2,3,4,5,6},若M={1,4},N={2,3},则∁U(M∪N)等于( )
| A. | {1,2,3,4} | B. | {3,4} | C. | {1,6} | D. | {5,6} |
2.已知椭圆$C:\frac{x^2}{12}+\frac{y^2}{3}=1$,直线l与椭圆C交于A,B两点,且线段AB的中点为M(-2,1),则直线l的斜率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
19.已知a=2${\;}^{-\frac{2}{3}}$,$b={({\frac{1}{2}})^{\frac{4}{3}}}$,$c={2^{-\frac{1}{3}}}$,则下列关系式中正确的是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | c<a<b |
20.下列说法中正确的是( )
| A. | “a>b”是“log2a>log2b”的充要条件 | |
| B. | 若函数y=sin2x的图象向左平移$\frac{π}{4}$个单位得到的函数图象关于y轴对称 | |
| C. | 命题“在△ABC中,$A>\frac{π}{3}$,则$sinA>\frac{{\sqrt{3}}}{2}$”的逆否命题为真命题 | |
| D. | 若数列{an}的前n项和为${S_n}={2^n}$,则数列{an}是等比数列 |
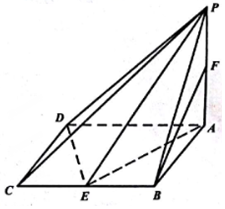 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=$\sqrt{3}$,PA⊥面ABCD,E、F分别为BC、PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA=$\sqrt{3}$,PA⊥面ABCD,E、F分别为BC、PA的中点.