题目内容
已知f(x)=px2-q,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围.
答案:
解析:
提示:
解析:
|
解:依题意,有 ∴ ∴f(3)=9p-q= ∵-1≤f(2)≤5,∴- -4≤f(1)≤-1,∴ ∴- 即-1≤f(3)≤20. 当 当 分析:可考虑将f(3)写成f(1)、f(2)的线性组合,即f(3)=mf(1)+nf(2)的形式,然后用不等式的运算性质推算f(3)的取值范围. |
提示:
|
注:这种类型的题目常见的错误是 由 1≤q≤7,从而-7≤f(3)=9p-q≤26. 事实上,f(3)不可能取得[-7,26]上的一切值,p、q是两个相互联系、相互制约的量,在得出0≤p≤3,1≤q≤7后,并不意味着p、q可以独立地取得区间[0,3]及[1,7]上的一切值.如取p=0,q=7时,p-q=-7,已不满足-4≤p-q≤-1. 所以用不等式的运算性质求范围时,尽量只用一次,如果需要多次使用性质时,要考虑等号能否取到,否则可能会出现范围过大或过小的情况. |

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目

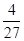 ,0
B.0,
,0
B.0,