题目内容
已知实数a＜2，则a+| 1 | a-2 |
分析：注意到实数a＜2，把函数解析式整理成基本不等式的形式，求得函数的最值和此时x的取值．
解答：解：a+
=a-2+
+2
=-(2-a+
)+2≤-2+2=0
当a-2=-1时，即a=1时等号成立．
则a+
的最 大值是0．
故答案为：大；0．
| 1 |
| a-2 |
=a-2+
| 1 |
| a-2 |
=-(2-a+
| 1 |
| 2-a |
当a-2=-1时，即a=1时等号成立．
则a+
| 1 |
| a-2 |
故答案为：大；0．
点评：本题主要考查函数最值的求法，一般有两种方法，一是函数法，二是基本不等式法，本题应用的是基本不等式法，要注意一正，二定，三相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
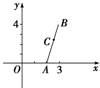如图所示，已知两点A（2，0），B（3，4），直线ax-2y=0与线段AB交于点C，且C分
的最 值是 ．