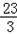题目内容
求 在区间[﹣1,3]的最值.
在区间[﹣1,3]的最值.
 在区间[﹣1,3]的最值.
在区间[﹣1,3]的最值.解:∵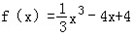
∴f′(x)=x2﹣4
令f′(x)=0,x∈[﹣1,3]可得x=2
∵当x∈[﹣1,2)时,f′(x)<0恒成立;
当x∈(2,3]时,f′(x)>0恒成立;
故当x=2时,函数f(x)有极(最)小值﹣
又∵f(﹣1)=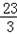 ,f(3)=1
,f(3)=1
故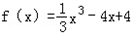 在区间[﹣1,3]的最小值为﹣
在区间[﹣1,3]的最小值为﹣ ,最大值为
,最大值为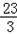

练习册系列答案
相关题目
题目内容
 在区间[﹣1,3]的最值.
在区间[﹣1,3]的最值.解:∵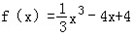
∴f′(x)=x2﹣4
令f′(x)=0,x∈[﹣1,3]可得x=2
∵当x∈[﹣1,2)时,f′(x)<0恒成立;
当x∈(2,3]时,f′(x)>0恒成立;
故当x=2时,函数f(x)有极(最)小值﹣
又∵f(﹣1)=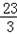 ,f(3)=1
,f(3)=1
故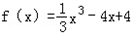 在区间[﹣1,3]的最小值为﹣
在区间[﹣1,3]的最小值为﹣ ,最大值为
,最大值为