题目内容
函数f(x)=4x-2x在区间[-2,1]上的值域为________.
[- ]
]
分析:令t=2x,则t ,而y=f(t)=t2-t=
,而y=f(t)=t2-t= ,结合二次函数的性质可求函数的值域
,结合二次函数的性质可求函数的值域
解答:令t=2x,则t
∴y=f(t)=t2-t= 在
在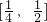 上单调递减,在[
上单调递减,在[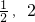 ]上单调递增
]上单调递增
∴当t= 时,函数有最小值
时,函数有最小值
∵f( )=
)= <f(2)=2
<f(2)=2
∴函数的值域[ ,2]
,2]
点评:本题主要考查了指数函数的性质及二次函数的性质在求解函数的值域中的应用,解题中要注意新元t的范围
 ]
]分析:令t=2x,则t
 ,而y=f(t)=t2-t=
,而y=f(t)=t2-t= ,结合二次函数的性质可求函数的值域
,结合二次函数的性质可求函数的值域解答:令t=2x,则t

∴y=f(t)=t2-t=
 在
在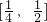 上单调递减,在[
上单调递减,在[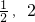 ]上单调递增
]上单调递增∴当t=
 时,函数有最小值
时,函数有最小值
∵f(
 )=
)= <f(2)=2
<f(2)=2∴函数的值域[
 ,2]
,2]点评:本题主要考查了指数函数的性质及二次函数的性质在求解函数的值域中的应用,解题中要注意新元t的范围

练习册系列答案
相关题目