题目内容
设函数 在区间
在区间 上可导,若
上可导,若 ,总有
,总有 ,则称
,则称 为区间
为区间 上的
上的 函数.在下列四个函数
函数.在下列四个函数 ,
, ,
, ,
, 中,在区间
中,在区间 上为
上为 函数的个数是
函数的个数是
A. | B. | C. | D.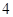 |
A
解析试题分析:根据题意,由于设函数 在区间
在区间 上可导,若
上可导,若 ,总有
,总有 ,则称
,则称 为区间
为区间 上的
上的 函数.那么在
函数.那么在 ,
, ,
, ,
, 中,在区间
中,在区间 上为
上为 函数,即说明函数式凹函数即可,那么可知在
函数,即说明函数式凹函数即可,那么可知在 的个数是只有二次函数
的个数是只有二次函数 满足题意,故答案为A.
满足题意,故答案为A.
考点:新定义
点评:主要是考查了函数的性质的运用,属于基础题。

练习册系列答案
相关题目
函数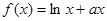 存在与直线
存在与直线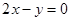 平行的切线,则实数
平行的切线,则实数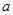 的取值范围是( )
的取值范围是( )
A.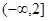 | B.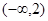 | C. | D. |
已知函数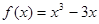 ,若过点
,若过点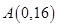 且与曲线
且与曲线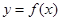 相切的切线方程为
相切的切线方程为 ,则实数
,则实数 的值是( )
的值是( )
A. | B.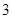 | C.6 | D.9 |
已知函数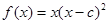 在
在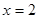 处有极大值,则
处有极大值,则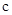 =( )
=( )
| A.6 | B.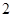 | C.2或6 | D.-2或6 |
曲线y=2sinx在点P(π,0)处的切线方程为 ( )
A.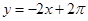 | B.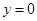 |
C.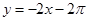 | D.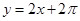 |
曲线 在点
在点 处的切线方程是
处的切线方程是
A. | B. | C. | D. |
已知函数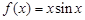 ,则
,则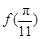 ,
,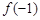 ,
,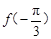 的大小关系为( )
的大小关系为( )
A.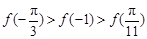 | B.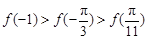 |
C.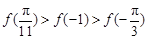 | D.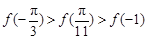 |
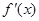 是函数f(x)的导函数,如果
是函数f(x)的导函数,如果
 ,那么曲线f(x)上任一点处的切线的倾斜角
,那么曲线f(x)上任一点处的切线的倾斜角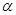 的取值范围是
的取值范围是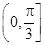

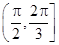

 为
为 ,那么,原油温度的瞬时变化率的最小值是( )
,那么,原油温度的瞬时变化率的最小值是( )

