题目内容
若数列{an}的前n项和Sn=n2+2n,若bn= ,记数列{bn}的前n项和为Tn,则使Tn>
,记数列{bn}的前n项和为Tn,则使Tn> 成立的最小正整数n的值为________.
成立的最小正整数n的值为________.
5
分析:利用an=Sn-Sn-1,即可确定数列{an}的通项,从而可得{bn}的通项,利用裂项法,即可求得结论.
解答:由题意,当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1
∵a1=S1=3,符合上式,∴an=2n+1
∴bn= =
= =
=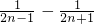
∴Tn= +…+
+…+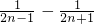 =
=
∵Tn> ,∴
,∴ >
>
∵2n>9,
∴使Tn> 成立的最小正整数n的值为5
成立的最小正整数n的值为5
故答案为:5
点评:本题考查数列的通项与求和,考查裂项法的运用,考查学生的计算能力,属于中档题.
分析:利用an=Sn-Sn-1,即可确定数列{an}的通项,从而可得{bn}的通项,利用裂项法,即可求得结论.
解答:由题意,当n≥2时,an=Sn-Sn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1
∵a1=S1=3,符合上式,∴an=2n+1
∴bn=
 =
= =
=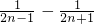
∴Tn=
 +…+
+…+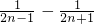 =
=
∵Tn>
 ,∴
,∴ >
>
∵2n>9,
∴使Tn>
 成立的最小正整数n的值为5
成立的最小正整数n的值为5故答案为:5
点评:本题考查数列的通项与求和,考查裂项法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
