Question

【题目】在平面直角坐标系xOy中，已知椭圆的左、右焦点分别为F1，F2，点A在椭圆E上且在第一象限内，AF2⊥F1F2，直线AF1与椭圆E相交于另一点B．

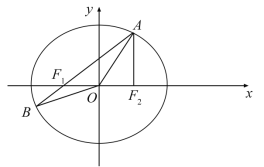
（1）求△AF1F2的周长；

（2）在x轴上任取一点P，直线AP与椭圆E的右准线相交于点Q，求的最小值；

（3）设点M在椭圆E上，记△OAB与△MAB的面积分别为S1，S2，若S2=3S1，求点M的坐标．

Answer 1

【答案】（1）6；（2）-4；（3）或.

【解析】

（1）根据椭圆定义可得，从而可求出的周长；

（2）设，根据点在椭圆上，且在第一象限，，求出，根据准线方程得点坐标，再根据向量坐标公式，结合二次函数性质即可出最小值；

（3）设出设，点到直线的距离为，由点到直线的距离与，可推出，根据点到直线的距离公式，以及满足椭圆方程，解方程组即可求得坐标.

（1）∵椭圆的方程为

∴,

由椭圆定义可得：.

∴的周长为

（2）设，根据题意可得.

∵点在椭圆上，且在第一象限，

∴

∵准线方程为

∴

∴，当且仅当时取等号.

∴的最小值为.

（3）设，点到直线的距离为.

∵，

∴直线的方程为

∵点到直线的距离为，

∴

∴

∴①

∵②

∴联立①②解得，.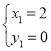

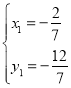∴或.