题目内容
已知椭圆 .过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点.
.过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点.(I)求椭圆G的焦点坐标和离心率;
(Ⅱ)将|AB|表示为m的函数,并求|AB|的最大值.
【答案】分析:(I)由题意及椭圆和圆的标准方程,利用椭圆离心率的定义和点到直线的距离公式即可求解;
(II)由题意即m得取值范围分m=1时,m=-1及当m≠±1三大类求出|AB|的长度,利用直线方程与椭圆方程进行联立,利用根与系数的关系得到k与m之间关系等式,利用
解答:解:(I)由题意得a=2,b=1,所以c=
∴椭圆G的焦点坐标 离心率e=
离心率e= .
.
(II)由题意知:|m|≥1,
当m=1时,切线l的方程为x=1,点A(1, ) 点B(1,-
) 点B(1,- ) 此时|AB|=
) 此时|AB|= ;
;
当m=-1时,同理可得|AB|= ;
;
当|m|>1时,设切线l的方程为:y=k(x-m),由 ⇒(1+4k2)x2-8k2mx+4k2m2-4=0,
⇒(1+4k2)x2-8k2mx+4k2m2-4=0,
设A(x1,y1),B(x2,y2)则x1+x2=
又由l与圆圆x2+y2=1相切∴圆心到直线l的距离等于圆的半径即 =1⇒m2=
=1⇒m2= ,
,
所以|AB|=
= =
= ,由于当m=±1时,|AB|=
,由于当m=±1时,|AB|= ,
,
当m≠±1时,|AB|= ,此时m∈(-∞,-1]∪[1,+∞)
,此时m∈(-∞,-1]∪[1,+∞)
又|AB|= ≤2(当且仅当m=±
≤2(当且仅当m=± 时,|AB|=2),
时,|AB|=2),
所以,|AB|的最大值为2.
故|AB|的最大值为2.
点评:此题重点考查了椭圆及圆的标准方程,还考查了点到直线的距离公式,对于第二问,重点考查了利用m的范围分裂进行讨论,联立直线与椭圆的方程利用整体代换的思想建立m与k的关系等式,还考查两点间的距离公式及又m的范围解出|AB|的最值.
(II)由题意即m得取值范围分m=1时,m=-1及当m≠±1三大类求出|AB|的长度,利用直线方程与椭圆方程进行联立,利用根与系数的关系得到k与m之间关系等式,利用
解答:解:(I)由题意得a=2,b=1,所以c=

∴椭圆G的焦点坐标
 离心率e=
离心率e= .
.(II)由题意知:|m|≥1,
当m=1时,切线l的方程为x=1,点A(1,
 ) 点B(1,-
) 点B(1,- ) 此时|AB|=
) 此时|AB|= ;
;当m=-1时,同理可得|AB|=
 ;
;当|m|>1时,设切线l的方程为:y=k(x-m),由
 ⇒(1+4k2)x2-8k2mx+4k2m2-4=0,
⇒(1+4k2)x2-8k2mx+4k2m2-4=0,设A(x1,y1),B(x2,y2)则x1+x2=

又由l与圆圆x2+y2=1相切∴圆心到直线l的距离等于圆的半径即
 =1⇒m2=
=1⇒m2= ,
,所以|AB|=

=
 =
= ,由于当m=±1时,|AB|=
,由于当m=±1时,|AB|= ,
,当m≠±1时,|AB|=
 ,此时m∈(-∞,-1]∪[1,+∞)
,此时m∈(-∞,-1]∪[1,+∞) 又|AB|=
 ≤2(当且仅当m=±
≤2(当且仅当m=± 时,|AB|=2),
时,|AB|=2),所以,|AB|的最大值为2.
故|AB|的最大值为2.
点评:此题重点考查了椭圆及圆的标准方程,还考查了点到直线的距离公式,对于第二问,重点考查了利用m的范围分裂进行讨论,联立直线与椭圆的方程利用整体代换的思想建立m与k的关系等式,还考查两点间的距离公式及又m的范围解出|AB|的最值.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,过点(m,0)作圆
,过点(m,0)作圆 的切线
的切线 交椭圆G于A,B两点.
交椭圆G于A,B两点. 表示为m的函数,并求
表示为m的函数,并求 的切线
的切线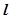 ,交椭圆G于A,B两点.
,交椭圆G于A,B两点. 表示为m的函数,并求
表示为m的函数,并求 .过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点.
.过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点. .过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点.
.过点(m,0)作圆x2+y2=1的切线I交椭圆G于A,B两点.