题目内容
已知两定点M(-1,0),N(1,0)若直线上存在点P,使得|PO|2=|PM|•|PN|(O为坐标原点),则该直线为“A型直线”.给出
下列直线,其中是“A型直线”的是( )
①y=x+1
②x=
③y=-x+3
④y=-2x+3.
下列直线,其中是“A型直线”的是( )
①y=x+1
②x=
| 1 |
| 2 |
③y=-x+3
④y=-2x+3.
分析:设P(x,y),根据|PO|2=|PM|•|PN|和两点的距离公式算出x2-y2=1,从而得到点P的轨迹是焦点在x轴上的等轴双曲线.由此,再判断①②③④中的直线与双曲线x2-y2=1是否有交点,即可得到“A型直线”的条数,得到本题的答案.
解答:解: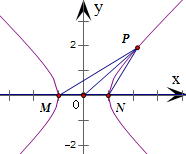 设P(x,y),可得|PO|2=x2+y2,
设P(x,y),可得|PO|2=x2+y2,
|PM|=
,|PN|=
∵|PO|2=|PM|•|PN|,
∴x2+y2=
•
,
化简整理,得x2-y2=1
∴点P的轨迹是x2-y2=1,是焦点在x轴上的等轴双曲线
对于①,因为直线y=x+1与双曲线x2-y2=1的渐近线y=x平行,
所以直线y=x+1与双曲线x2-y2=1必定有一个交点,
即存在点P,使得y=x+1是“A型直线”;
对于②,因为直线x=
过双曲线虚轴上一点与轴虚垂直,所以直线x=
与双曲线x2-y2=1没有交点
故不存在点P,使得x=
是“A型直线”;
对于③,因为直线y=-x+3与双曲线x2-y2=1的渐近线y=-x平行,所以直线y=-x+3与双曲线x2-y2=1必定有一个交点,
即存在点P,使得y=-x+3是“A型直线”;
对于④,因为直线y=-2x+3经过x轴上点(
,0),该点在双曲线x2-y2=1的张口以内
所以直线y=-2x+3与双曲线x2-y2=1必定有一个交点,即存在点P,使得y=-x+3是“A型直线”
综上所述,满足是“A型直线”的有①③④,共3个
故选:D
 设P(x,y),可得|PO|2=x2+y2,
设P(x,y),可得|PO|2=x2+y2,|PM|=
| (x+1)2+y2 |
| (x-1)2+y2 |
∵|PO|2=|PM|•|PN|,
∴x2+y2=
| (x+1)2+y2 |
| (x-1)2+y2 |
化简整理,得x2-y2=1
∴点P的轨迹是x2-y2=1,是焦点在x轴上的等轴双曲线
对于①,因为直线y=x+1与双曲线x2-y2=1的渐近线y=x平行,
所以直线y=x+1与双曲线x2-y2=1必定有一个交点,
即存在点P,使得y=x+1是“A型直线”;
对于②,因为直线x=
| 1 |
| 2 |
| 1 |
| 2 |
故不存在点P,使得x=
| 1 |
| 2 |
对于③,因为直线y=-x+3与双曲线x2-y2=1的渐近线y=-x平行,所以直线y=-x+3与双曲线x2-y2=1必定有一个交点,
即存在点P,使得y=-x+3是“A型直线”;
对于④,因为直线y=-2x+3经过x轴上点(
| 3 |
| 2 |
所以直线y=-2x+3与双曲线x2-y2=1必定有一个交点,即存在点P,使得y=-x+3是“A型直线”
综上所述,满足是“A型直线”的有①③④,共3个
故选:D
点评:本题给出满足条件的动点的轨迹,叫我们寻找“A型直线”的条数.着重考查了动点轨迹的求法、双曲线的几何性质和直线与双曲线位置关系等知识,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目