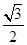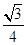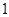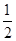题目内容
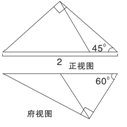
某空间几何体的三视图及尺寸如图1，则该几何体的体积是
A． | B． | C． | D． |
A
解析试题分析：由三视图可知该几何体是直三棱柱，底面为直角三角形，两直角边为1和2，侧棱长为2，所以体积为
考点：三视图与几何体体积
点评：先由三视图特征还原出几何体，再代入相应的体积公式求解，三视图是新课标高考必考内容
练习册系列答案
名校课堂系列答案
相关题目
已知某几何体的三视图如图，其中正视图中半圆的半径为1，则该几何体的体积为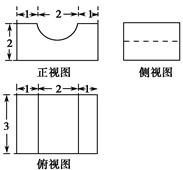
A．24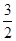－ π | B．24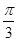－ | C．24－π | D．24－ |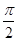
已知一个棱长为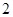
的正方体，被一个平面截后所得几何体的三视图如图所示，则该几何体的体积是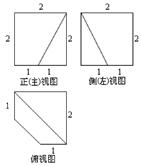
| A．8 | B． |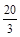
C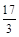． | D． |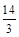
一个几何体的三视图如右图所示，则它的体积为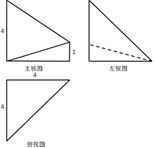
A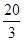． | B． |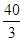
C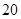． | D． |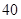
一个体积为
的正方体的顶点都在球面上，则球的体积是（ ）
A． | B． | C． | D． |
一个几何体的三视图如图所示,则该几何体的体积为 ( ) 
A． | B． | C． | D． |
已知某四棱锥的三视图（单位：cm）如图所示，则该四棱锥的体积是
A． | B． | C． | D． |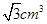
一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形. 则该几何体的体积为（ ）
| A．16 | B．48 |
| C．60 | D．96 |