题目内容
10. 如图,在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M在侧棱SC上,∠ABM=60°.若以DA,DC,DS,分别为x轴,y轴,z轴建立如图所示的空间直角坐标系D-xyz,则M的坐标为(0,1,1).
如图,在四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M在侧棱SC上,∠ABM=60°.若以DA,DC,DS,分别为x轴,y轴,z轴建立如图所示的空间直角坐标系D-xyz,则M的坐标为(0,1,1).
分析 设出空间直角坐标系,推出相关点的坐标,设出M坐标,利用空间向量的数量积求解即可.
解答  解:∵SD⊥底面ABCD,底面ABCD为矩形,
解:∵SD⊥底面ABCD,底面ABCD为矩形,
∴DA,DC,DS两两垂直,
如图以D为原点,直线DA,DC,DS分别为x,y,z轴,建立空间直角坐标系.
则D(0,0,0),B($\sqrt{2}$,2,0),S(0,0,2),C(0,2,0),$\overrightarrow{BA}$=(0,-2,0).$\overrightarrow{CS}$=(0,-2,2).$\overrightarrow{BA}=(0,-2,0)$,$\overrightarrow{BC}=(-\sqrt{2},0,0)$
设$\overrightarrow{CM}$=$λ\overrightarrow{CS}$=(0,-2λ,2λ).$\overrightarrow{BM}$=$\overrightarrow{BC}$+$\overrightarrow{CM}$=(-$\sqrt{2}$,-2λ,2λ).
∠ABM=60°.可得:cos60°=$\frac{\overrightarrow{BA}•\overrightarrow{BM}}{\overrightarrow{|BA}\left|\right|\overrightarrow{BM|}}$=$\frac{|4λ|}{2•\sqrt{2+(-2{λ)}^{2}+4{λ}^{2}}}$=$\frac{1}{2}$,
解得λ=$\frac{1}{2}$.$\overrightarrow{CM}$=(0,-1,1),$\overrightarrow{DM}$=(0,1,1)
M(0,1,1).
故答案为:(0,1,1).
点评 本题考查空间向量数量积的应用,空间点的坐标的求法,考查计算能力.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. | (kπ-$\frac{π}{2}$,kπ)(k∈Z) | B. | (kπ,kπ+$\frac{π}{2}$)(k∈Z) | C. | (kπ-$\frac{π}{4}$,kπ+$\frac{π}{4}$)(k∈Z) | D. | (kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$)(k∈Z) |
| A. | $\overrightarrow{CN}$ | B. | $\overrightarrow{BC}$ | C. | $\overrightarrow{C{C}_{1}}$ | D. | $\overrightarrow{{B}{C}_{1}}$ |
| A. | an=a1+d(n+1) | B. | an=a1+dn | C. | an=a1+d(n-1) | D. | an=a1+d(n-2) |
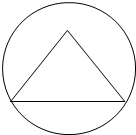 棱长为3的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,求图中三角形的面积、该球的表面积和体积.
棱长为3的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,求图中三角形的面积、该球的表面积和体积.