题目内容

求证: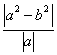≥|a|-|b|.

证法一:(分析法)?

(1)当b=0时,不等式显然成立.?

(2)当b≠0时,∵|a|＞0,?

只需证明|a2-b2|≥|a|2-|a||b|,两边同除以|b|2,?

即只需证明≥,?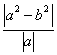

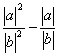即|()2-1|≥|()2|-||.?

当||≥1时,?

|()2-1|=|()2|-1≥||2-||,?

原不等式成立.?

当||＜1时,|a|-|b|＜0,?

原不等式成立.?

综上所述,原不等式成立.

证法二:(综合法)?

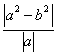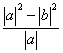∵≥=(|a|+|b|)=||a|-|b||(1+)≥||a|-|b||≥|a|-|b|.

练习册系列答案
相关题目
已知a＞
1
3
，b＞
1
3
，ab=
2
9
，求证a+b＜1．
已知向量
a
=(cosx，sinx)，
b
=(sinx，cosx)，且x∈[0，
π
2
]，
（1）求
a
•
b
的取值范围；
（2）求证|
a
+
b
|=2sin(x+
π
4
)；
（3）求函数f(x)=
a
•
b
-
2
|
a
+
b
|的取值范围．
（文科做）已知A、B都是锐角，且A+B≠
π2
，（1+tanA）（1+tanB）=2，求证A+B=45°．
对于一般的三次函数f（x）=ax3+bx2+cx+d，（a≠0）定义：设f''（x）是函数y=f（x）的导函数y=f'（x）的导数．若f''（x）=0有实数解x0，则称点（x0，f（x0））为函数y=f（x）的“拐点”，现已知：g（x）=（x-a）（x-b）（x-c），请解答下列问题：
（Ⅰ）．若y=g（x）是R上的增函数，求证a=b=c；
（Ⅱ）在（Ⅰ）．的条件下，求函数y=g（x）的“拐点”A的坐标，并证明函数y=g（x）的图象关于“拐点”A成中心对称．
已知向量
a
=(
3
2
，-
1
2
)，
b
=(1，
3
)．
（Ⅰ）求证
a
⊥
b
；
（Ⅱ）如果对任意的s∈R+，使
m
=
a
+(1+2s)
b
与
n
=-k
a
+(1+
1
s
)
b
垂直，求实数k的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网