题目内容
(9分)无论![]() 为任何实数,直线
为任何实数,直线![]() 与双曲线
与双曲线![]() :
:![]() 且
且![]() 恒有公共点
恒有公共点
(Ⅰ)求双曲线![]() 的离心率
的离心率![]() 的取值范围;
的取值范围;
(Ⅱ)若直线![]() 过双曲线
过双曲线![]() 的右焦点
的右焦点![]() ,与双曲线
,与双曲线![]() 交于
交于![]() 、
、![]() 两点,并且
两点,并且![]() 求双曲线
求双曲线![]() 的方程.
的方程.
(9分)
解:(Ⅰ)联立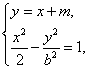 得
得![]() (*)
(*)
当![]() 时,方程
时,方程![]() ,当
,当![]() 时方程组无解,即直线
时方程组无解,即直线![]() 与C无交点,与
与C无交点,与![]() 、C恒有交点矛盾.
、C恒有交点矛盾.
当![]() 时,方程(*)中
时,方程(*)中![]() 对实数
对实数![]() 恒成立,即
恒成立,即
![]() 即
即![]() 对实数
对实数![]() 恒成立,
恒成立,
∵![]() ∴
∴![]() 对
对![]() 恒成立,
恒成立,![]() ,又
,又![]() ,
,
∴![]() ∴
∴![]() ∴
∴![]() (4分)
(4分)
(Ⅱ)设![]() ,由
,由![]() 得
得![]()
∴![]()
由方程(*)得![]()
将![]() 代人上面两个方程,得
代人上面两个方程,得![]()
∵直线![]() 过双曲线C的右焦点F,∴
过双曲线C的右焦点F,∴![]() ∴
∴![]()
∴![]() ∴双曲线C的方程为
∴双曲线C的方程为 ![]() (9分)
(9分)

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
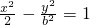 (b>0)恒有公共点
(b>0)恒有公共点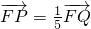 ,求双曲线C的方程.
,求双曲线C的方程.