题目内容
已知函数![]() .
.
(Ⅰ)求函数f(x)的最小正周期和值域;
(Ⅱ)若a为第二象限角,且![]() ,求
,求![]() 的值.
的值.
考点:
三角函数中的恒等变换应用;三角函数的恒等变换及化简求值;三角函数的周期性及其求法.
专题:
综合题.
分析:
(Ⅰ)利用二倍角公式及辅助角公式化简函数,从而可求函数f(x)的最小正周期和值域;
(Ⅱ)利用![]() ,求得cosα的值,利用α为第二象限角,可求sinα的值,进而可得
,求得cosα的值,利用α为第二象限角,可求sinα的值,进而可得![]() 的值.
的值.
解答:
解:(Ⅰ)![]() =
=![]() =1+2cos(x+
=1+2cos(x+![]() )
)
∴函数f(x)的周期为2π,
∵2cos(x+![]() )∈[﹣2,2],∴函数的值域为[﹣1,3]. …(5分)
)∈[﹣2,2],∴函数的值域为[﹣1,3]. …(5分)
(Ⅱ)因为![]() ,所以1+2cosα=
,所以1+2cosα=![]() ,即cosα=﹣
,即cosα=﹣![]() . …(6分)
. …(6分)
因为α为第二象限角,所以sinα=![]() .
.
所以![]() =cosα(cosα+sinα)=﹣
=cosα(cosα+sinα)=﹣![]() ×(﹣
×(﹣![]() +
+![]() )=
)=![]() …(13分)
…(13分)
点评:
本题考查三角函数的化简,考查函数的性质,考查函数值的计算,解题的关键是化简函数.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.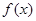 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求