题目内容
已知数列{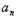 }的前n项和为
}的前n项和为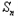 ,且满足a1=1,
,且满足a1=1,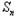 =t
=t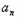 +1 (n∈N+,t∈R).
+1 (n∈N+,t∈R).
(1)求数列{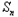 }的通项公式;
}的通项公式;
(2)求数列{n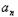 }的前n项和为Tn.
}的前n项和为Tn.
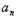 }的前n项和为
}的前n项和为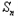 ,且满足a1=1,
,且满足a1=1,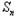 =t
=t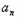 +1 (n∈N+,t∈R).
+1 (n∈N+,t∈R).(1)求数列{
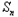 }的通项公式;
}的通项公式;(2)求数列{n
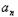 }的前n项和为Tn.
}的前n项和为Tn.解:(1)∵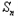 =t
=t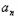 +1,
+1,
∴当n=1时,S1=ta2=a1=1,
∴t≠0,
又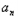 +1=
+1=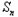 +1﹣
+1﹣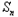 ,
,
∴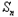 =t(
=t(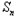 +1﹣
+1﹣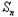 ),
),
∴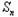 +1=
+1=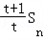 ,
,
∴当t=﹣1时,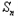 +1=0,S1=a1=0,
+1=0,S1=a1=0,
当t≠﹣1时,数列{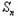 }是等比数列,
}是等比数列,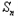 =
= ,
,
综上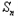 =
=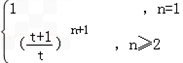 .
.
(2)∵Tn=a1+2a2+3a3+…+n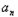 ①
①
∴T1=1,n≥2时又由①可知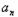 +1=
+1=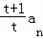 ,a2=
,a2= ,
,
∴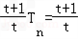 a1+2a3+3a4+…+n
a1+2a3+3a4+…+n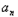 +1 ②
+1 ②
①﹣②得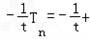 2a2+a3+a4+…+
2a2+a3+a4+…+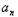 ﹣n
﹣n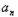 +1
+1
=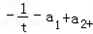 (a1+a2+a3+…+
(a1+a2+a3+…+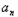 )﹣n
)﹣n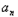 +1
+1
=﹣1+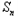 ﹣n(
﹣n(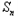 +1﹣
+1﹣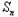 )
)
=﹣1+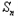 ﹣
﹣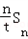 .
.
Tn=t﹣t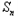 +n
+n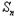 =
=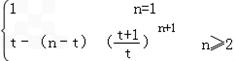 .
.
 =t
=t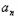 +1,
+1,∴当n=1时,S1=ta2=a1=1,
∴t≠0,
又
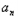 +1=
+1=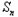 +1﹣
+1﹣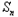 ,
,∴
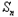 =t(
=t(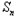 +1﹣
+1﹣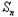 ),
),∴
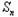 +1=
+1=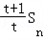 ,
,∴当t=﹣1时,
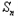 +1=0,S1=a1=0,
+1=0,S1=a1=0,当t≠﹣1时,数列{
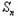 }是等比数列,
}是等比数列,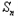 =
= ,
,综上
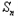 =
=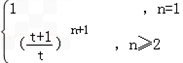 .
.(2)∵Tn=a1+2a2+3a3+…+n
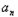 ①
①∴T1=1,n≥2时又由①可知
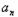 +1=
+1=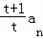 ,a2=
,a2= ,
,∴
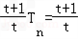 a1+2a3+3a4+…+n
a1+2a3+3a4+…+n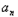 +1 ②
+1 ②①﹣②得
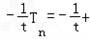 2a2+a3+a4+…+
2a2+a3+a4+…+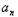 ﹣n
﹣n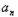 +1
+1=
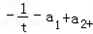 (a1+a2+a3+…+
(a1+a2+a3+…+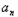 )﹣n
)﹣n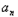 +1
+1=﹣1+
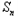 ﹣n(
﹣n(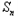 +1﹣
+1﹣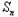 )
)=﹣1+
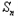 ﹣
﹣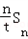 .
.Tn=t﹣t
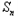 +n
+n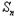 =
=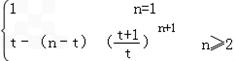 .
.
练习册系列答案
相关题目