题目内容
设Sn为数列{an}的前n项和,对任意的n∈N*,都有Sn=(m+1)-man(m为常数,且m>0)。
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足b1=2a1,bn=f(bn-1)(n≥2,n∈N*),求数列{bn}的通项公式;
(3)在满足(2)的条件下,求数列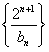 的前n项和Tn。
的前n项和Tn。
(1)求证:数列{an}是等比数列;
(2)设数列{an}的公比q=f(m),数列{bn}满足b1=2a1,bn=f(bn-1)(n≥2,n∈N*),求数列{bn}的通项公式;
(3)在满足(2)的条件下,求数列
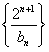 的前n项和Tn。
的前n项和Tn。 (1)证明:当n=1时,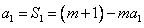 ,解得
,解得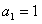 ;
;
当n≥2时,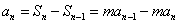 , 即
, 即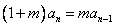 ,
,
∵m为常数,且m>0,∴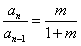 (n≥2),
(n≥2),
∴数列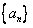 是首项为1,公比为
是首项为1,公比为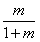 的等比数列。
的等比数列。
(2)解:由(1)得,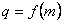
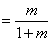 ,
,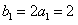 ,
,
∵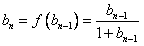 ,
,
∴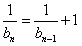 ,即
,即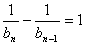
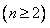 ,
,
∴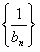 是首项为
是首项为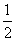 ,公差为1的等差数列,
,公差为1的等差数列,
∴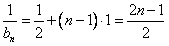 ,即
,即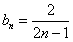 (n∈N*)。
(n∈N*)。
(3)解:由(2)知,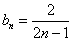 ,则
,则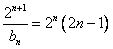 ,
,
所以,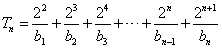 ,
,
即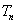
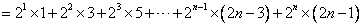 , ①
, ①
则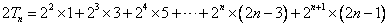 , ②
, ②
②-①得,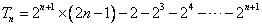 ,
,
故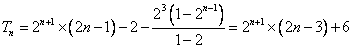 。
。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目