Question

（1）在极坐标系中，曲线C₁的方程为ρ=2cosθ，曲线C₂的方程为ρcosθ=2，则C₁与C₂的交点个数为

1

．
（2）对于实数x，y，若|x-1|≤1，|y-1|≤1，则使得|x-2y+1|-m-1≤0恒成立的实数m的最小值为

2

．

Answer 1

分析：（1）已知曲线C₁，C₂的极坐标方程，可将圆C和直线C₂先化为一般方程坐标，然后再计算曲线C₁与C₂交点的个数．
（2）首先分析题目已知不等式|x-2y+1|-m-1≤0恒成立的实数m的最小值，故可以考虑设y=|x-2y+1|，然后利用线性规划的方法，求解出函数y=|x-2y+1|，的最大值，然后把m+1大于等于最小值，即可满足条件．

解答：解：（1）∵曲线C₁，C₂的极坐标方程分别为ρ=2cosθ，ρcosθ=2，
又x=ρcosθ，y=ρsinθ，分别代入消去ρ和θ，可得，
x²+y²=2x，和x=2
∴把x=2代入x²+y²=2x得，
y=0，
∴曲线C₁与C₂交点的个数为1个．
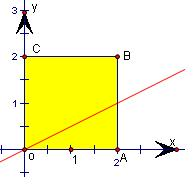（2）设y=|x-2y+1|，画出|x-1|≤1，|y-1|≤1，表示的区域，得正方形的四个顶点O（0，0），A（2，0），B（2，2），C（0，2）
当x=2，y=0时，x-2y+1=3，
当x=0，y=2时，x-2y+1=-3，
故y=|x-2y+1|∈[0，3]，其有最大值3．
不等式|x-2y+1|-m-1≤0恒成立，即|x-2y+1|≤m+1，
也即m+1必大于等于y=|x-2y+1|的最大值3．即m+1≥3，m≥2
故实数m的最小值为：2．
故答案为：1；2．

点评：（1）此小题考查极坐标方程与普通方程的区别和联系，两者要会互相转化，根据实际情况选择不同的方程进行求解，这也是每年高考必考的热点问题．
（2）此题主要考查绝对值不等式恒成立的解法问题，其中涉及到数形结合的思想，属于基础性题目．