题目内容
设函数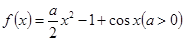 .
.
(1)当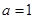 时,求函数
时,求函数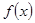 在
在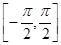 上的最大值和最小值;
上的最大值和最小值;
(2)若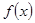 在
在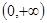 上为增函数,求正数
上为增函数,求正数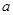 的取值范围.
的取值范围.
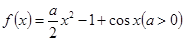 .
.(1)当
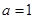 时,求函数
时,求函数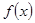 在
在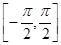 上的最大值和最小值;
上的最大值和最小值;(2)若
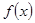 在
在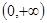 上为增函数,求正数
上为增函数,求正数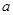 的取值范围.
的取值范围.(1)最小值为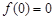 ,最大值为
,最大值为 ;(2)
;(2)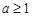 .
.
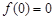 ,最大值为
,最大值为 ;(2)
;(2)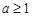 .
.试题分析:(1)当
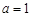 时,
时,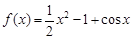 ,其导函数
,其导函数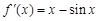 ,易得当
,易得当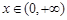 时,
时,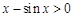 ,即函数
,即函数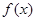 在区间
在区间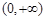 上单调递增,又函数
上单调递增,又函数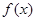 是偶函数,所以函数
是偶函数,所以函数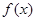 在
在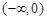 上单调递减,
上单调递减,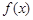 在
在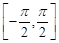 上的最小值为
上的最小值为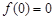 ,最大值为
,最大值为 ;
;(2)由题得:
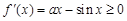 在
在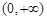 上恒成立,易证
上恒成立,易证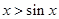 ,若
,若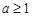 时,则
时,则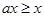 ,所以
,所以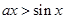 ;若
;若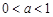 时,易证此时不成立.
时,易证此时不成立.(1)当
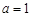 时,
时,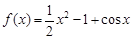 ,
, 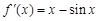 ,
,令
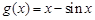 ,则
,则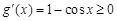 恒成立,
恒成立,∴
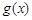 为增函数,
为增函数, 故当
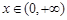 时,
时,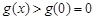
∴当
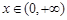 时,
时,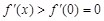 ,∴
,∴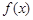 在
在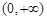 上为增函数,
上为增函数,又
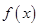 为偶函数,
为偶函数,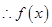 在
在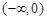 上为减函数,
上为减函数, ∴
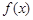 在
在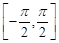 上的最小值为
上的最小值为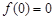 ,最大值为
,最大值为 .
.(2)由题意,
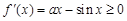 在
在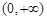 上恒成立.
上恒成立.(ⅰ)当
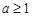 时,对
时,对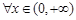 ,恒有
,恒有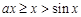 ,此时
,此时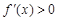 ,函数
,函数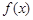 在
在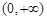 上为增函数,满足题意;
上为增函数,满足题意; (ⅱ)当
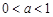 时,令
时,令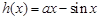 ,
,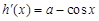 ,由
,由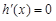 得
得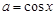 ,
,一定
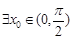 ,使得
,使得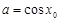 ,且当
,且当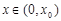 时,
时,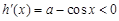 ,
,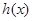 在
在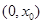 上单调递减,此时
上单调递减,此时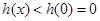 ,即
,即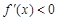 ,所以
,所以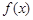 在
在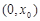 为减函数,这与
为减函数,这与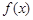 在
在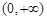 为增函数矛盾.
为增函数矛盾.综上所述:
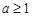 .
. 
练习册系列答案
相关题目
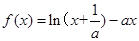 ,其中
,其中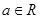 且
且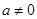 .
.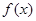 的单调性;
的单调性;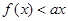 恒成立,求实数
恒成立,求实数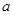 取值范围;
取值范围;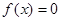 存在两个异号实根
存在两个异号实根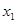 ,
,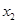 ,求证:
,求证: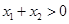
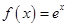 .
.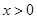 时,设
时,设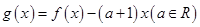 .讨论函数
.讨论函数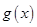 的单调性;
的单调性;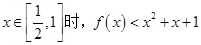 .
.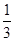 x3-
x3-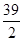 x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________.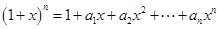 ,
,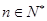 且
且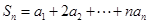 ,
, 时,
时,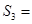 ; 当
; 当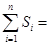 .
.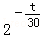 ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )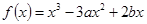 在x=1处有极小值-1,
在x=1处有极小值-1,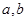 的值; (2)求出
的值; (2)求出 的单调区间.
的单调区间.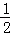 x2﹣lnx的单调递减区间为( )
x2﹣lnx的单调递减区间为( )