题目内容
已知正数x,y,z满足5x+4y+3z=10.
(1)求证: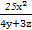
+
+
≥5.
(2)求
+
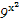的最小值.
(1)求证:
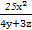++≥5.(2)求
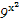+的最小值.(1)见解析 (2) 18
(1)根据柯西不等式,得
[(4y+3z)+(3z+5x)+(5x+4y)](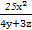++)≥(5x+4y+3z)2,
当且仅当
=
=
,
即x=
,y=
,z=
时取等号.
因为5x+4y+3z=10,
所以++≥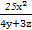
=5.
(2)根据平均值不等式,得
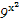+≥2
=2·
,
当且仅当x2=y2+z2时,等号成立.
根据柯西不等式,得
(x2+y2+z2)(52+42+32)≥(5x+4y+3z)2=100,
即x2+y2+z2≥2,当且仅当
=
=
时,
等号成立.
综上,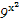+≥2·32=18.
当且仅当x=1,y=
,z=
时,等号成立.
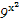所以+的最小值为18.
[(4y+3z)+(3z+5x)+(5x+4y)](
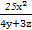++)≥(5x+4y+3z)2,当且仅当
==,即x=
,y=,z=时取等号.因为5x+4y+3z=10,
所以
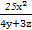++≥=5.(2)根据平均值不等式,得
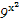+≥2=2·,当且仅当x2=y2+z2时,等号成立.
根据柯西不等式,得
(x2+y2+z2)(52+42+32)≥(5x+4y+3z)2=100,
即x2+y2+z2≥2,当且仅当
==时,等号成立.
综上,
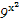+≥2·32=18.当且仅当x=1,y=
,z=时,等号成立.所以
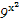+的最小值为18.
练习册系列答案
相关题目
.
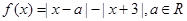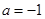时，解不等式
；
时，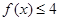
，求a的取值范围.
+
≥a+b.
假定该产品产销平衡，那么根据上述统计规律求下列问题．
>1的一个充分不必要条件是( )
≥0的解集为________．
∈A，
∉A.
<1
)a<(