题目内容
设 ,则“
,则“ ”是“
”是“ ”的 ( )
”的 ( )
| A.充分而不必要条件; | B.必要而不充分条件; |
| C.充分必要条件; | D.既不充分也不必要条件; |
B
解析试题分析: 即
即 ,显然
,显然 ,所以“
,所以“ ”是“
”是“ ”的必要而不充分条件;选B.
”的必要而不充分条件;选B.
考点:本题主要考查充要条件的概念,简单绝对值不等式的解法。
点评:简单题,理解好充要条件的概念是关键。这里利用了集合关系法判断。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
命题“所有实数的平方都是正数”的否定为
| A.所有实数的平方都不是正数 | B.有的实数的平方是正数 |
| C.至少有一个实数的平方是正数 | D.至少有一个实数的平方不是正数 |
若a,b∈R,则a>b>0是a2>b2的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
若 是真命题,
是真命题, 是假命题,则( )
是假命题,则( )
A. 是真命题 是真命题 | B. 是假命题 是假命题 |
C. 是真命题 是真命题 | D. 是真命题 是真命题 |
已知命题 ,使得
,使得 ;
; ,使得
,使得 .以下命题为真命题的为 ( )
.以下命题为真命题的为 ( )
A. | B. | C. | D. |
设 是
是 的三内角,则“
的三内角,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 ,则
,则 是
是 的
的
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 在
在 时是增函数,
时是增函数, 也是增函数,所以
也是增函数,所以 与
与 轴没有交点,则
轴没有交点,则 且
且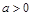 ;(3)
;(3) 的递增区间为
的递增区间为 ;(4)
;(4) 和
和 表示相等函数。
表示相等函数。 ,现给出下列命题:
,现给出下列命题: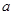 =
= ;
; 在
在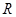 上是增函数;
上是增函数;  时,不等式
时,不等式 恒成立;
恒成立; 是偶函数.
是偶函数.