题目内容
如图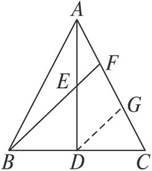
图
求证:AF=![]() AC.
AC.
思路分析:欲证AF=![]() AC,只要取FC的中点G,然后证AF=FG=GC即可,或者过D作DG∥BF,再证AF=FG=GC.
AC,只要取FC的中点G,然后证AF=FG=GC即可,或者过D作DG∥BF,再证AF=FG=GC.
证法一:取FC中点G,∵BD=DC,
∴DG为△BFC的中位线.∴DG∥EF.
在△ADG中,E为AD中点,∴F为AG中点.∴AF=FG=GC.∴AF=![]() AC.
AC.
证法二:过D作DG∥BF交AC于G.
在△ADG中,E为AD中点,∴AF=FG.
在△BCF中,D为BC中点,∴FG=GC.
∴AF=FG=GC.∴AF=![]() AC.
AC.

练习册系列答案
相关题目