题目内容
20.已知△ABC的面积为4,点E、F分别在边AB、AC上,且$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{BC}$,若P为线段EF上一动点,则$\overrightarrow{PB}$•$\overrightarrow{PC}$+$\overrightarrow{BC}$2的最小值为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{3\sqrt{6}}{2}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 3$\sqrt{3}$ |
分析 根据△ABC的面积为4,可得△PBC的面积=$\frac{4}{3}$,从而可得PB×PC=$\frac{8}{3sin∠BPC}$,故$\overrightarrow{PC}•\overrightarrow{PB}$=PB×PCcos∠BPC=$\frac{8cos∠BPC}{3sin∠BPC}$,由余弦定理,
得到BC2=BP2+CP2-2BP×CPcos∠BPC,进而可得BC2≥2BP×CP-2BP×CPcos∠BPC.从而$\overrightarrow{PC}•\overrightarrow{PB}+{\overrightarrow{BC}}^{2}≥$$\frac{16-8cos∠BPC}{3sin∠BPC}$.然后利用导数求得$\frac{16-8cos∠BPC}{3sin∠BPC}$的最大值可得$\overrightarrow{PB}$•$\overrightarrow{PC}$+$\overrightarrow{BC}$2的最小值.
解答 解:∵E、F分别在边AB、AC上,且$\overrightarrow{EF}$=$\frac{2}{3}$$\overrightarrow{BC}$,
∴△ABC的面积=3△PBC的面积,而△ABC的面积=4,∴△PBC的面积=$\frac{4}{3}$,
即$\frac{1}{2}PB•PC•sin∠BPC=\frac{4}{3}$,PB×PC=$\frac{8}{3sin∠BPC}$,
∴$\overrightarrow{PC}•\overrightarrow{PB}$=PB×PCcos∠BPC=$\frac{8cos∠BPC}{3sin∠BPC}$,
由余弦定理,BC2=BP2+CP2-2BP×CPcos∠BPC,
∵BP,CP均为正数,则BP2+CP2≥2BP×CP,
∴BC2≥2BP×CP-2BP×CPcos∠BPC.
则$\overrightarrow{PB}$•$\overrightarrow{PC}$+$\overrightarrow{BC}$2≥PB×PCcos∠BPC+2BP×CP-2BP×CPcos∠BPC=$\frac{16-8cos∠BPC}{3sin∠BPC}$.
令y=$\frac{16-8cos∠BPC}{3sin∠BPC}$,则$y′=\frac{24si{n}^{2}∠BPC-48coc∠BPC+24co{s}^{2}∠BPC}{9si{n}^{2}∠BPC}$=$\frac{24-48cos∠BPC}{9si{n}^{2}∠BPC}$.
由y′=0,得cos$∠BPC=\frac{1}{2}$.
此时函数在(0,$\frac{1}{2}$)上单调增,在($\frac{1}{2}$,1)上单调减,
∴cos∠BPC=$\frac{1}{2}$时,$\frac{16-8cos∠BPC}{3sin∠BPC}$取得最大值为$\frac{8\sqrt{3}}{3}$.
∴$\overrightarrow{PB}$•$\overrightarrow{PC}$+$\overrightarrow{BC}$2的最小值为$\frac{8\sqrt{3}}{3}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查三角形面积的计算,考查导数知识的运用,综合性强,属难题.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案| A. | 27 | B. | 81 | C. | 243 | D. | 729 |
| A. | 1:6 | B. | 1:5 | C. | 1:4 | D. | 1:3 |
| A. | $\frac{3\sqrt{22}}{14}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{22}}{14}$或$\frac{\sqrt{6}}{2}$ |
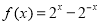 ,数列
,数列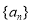 满足
满足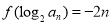 .
.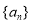 的通项公式;
的通项公式;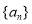 是递减数列.
是递减数列.